|
My Project
0.0.16
QUCS Mapping
|
|
My Project
0.0.16
QUCS Mapping
|
Dense matrix class implementation. More...
#include <assert.h>#include <stdio.h>#include <stdlib.h>#include <string.h>#include <math.h>#include "logging.h"#include "object.h"#include "complex.h"#include "vector.h"#include "matrix.h"
Go to the source code of this file.
Functions | |
| matrix | operator+ (matrix a, matrix b) |
| Matrix addition. | |
| matrix | operator- (matrix a, matrix b) |
| Matrix subtraction. | |
| matrix | operator* (matrix a, nr_complex_t z) |
| Matrix scaling complex version. | |
| matrix | operator* (nr_complex_t z, matrix a) |
| Matrix scaling complex version (different order) | |
| matrix | operator* (matrix a, nr_double_t d) |
| Matrix scaling complex version. | |
| matrix | operator* (nr_double_t d, matrix a) |
| Matrix scaling real version (different order) | |
| matrix | operator/ (matrix a, nr_complex_t z) |
| Matrix scaling division by complex version. | |
| matrix | operator/ (matrix a, nr_double_t d) |
| Matrix scaling division by real version. | |
| matrix | operator* (matrix a, matrix b) |
| matrix | operator+ (matrix a, nr_complex_t z) |
| Complex scalar addition. | |
| matrix | operator+ (nr_complex_t z, matrix a) |
| Complex scalar addition different order. | |
| matrix | operator+ (matrix a, nr_double_t d) |
| Real scalar addition. | |
| matrix | operator+ (nr_double_t d, matrix a) |
| Real scalar addition different order. | |
| matrix | operator- (matrix a, nr_complex_t z) |
| Complex scalar substraction. | |
| matrix | operator- (nr_complex_t z, matrix a) |
| Complex scalar substraction different order. | |
| matrix | operator- (matrix a, nr_double_t d) |
| Real scalar substraction. | |
| matrix | operator- (nr_double_t d, matrix a) |
| Real scalar substraction different order. | |
| matrix | transpose (matrix a) |
| Matrix transposition. | |
| matrix | conj (matrix a) |
| Conjugate complex matrix. | |
| matrix | adjoint (matrix a) |
| adjoint matrix | |
| matrix | abs (matrix a) |
| Computes magnitude of each matrix element. | |
| matrix | dB (matrix a) |
| Computes magnitude in dB of each matrix element. | |
| matrix | arg (matrix a) |
| Computes the argument of each matrix element. | |
| matrix | real (matrix a) |
| Real part matrix. | |
| matrix | imag (matrix a) |
| Imaginary part matrix. | |
| matrix | eye (int rs, int cs) |
| Create identity matrix with specified number of rows and columns. | |
| matrix | eye (int s) |
| Create a square identity matrix. | |
| matrix | diagonal (vector diag) |
| Create a diagonal matrix from a vector. | |
| matrix | pow (matrix a, int n) |
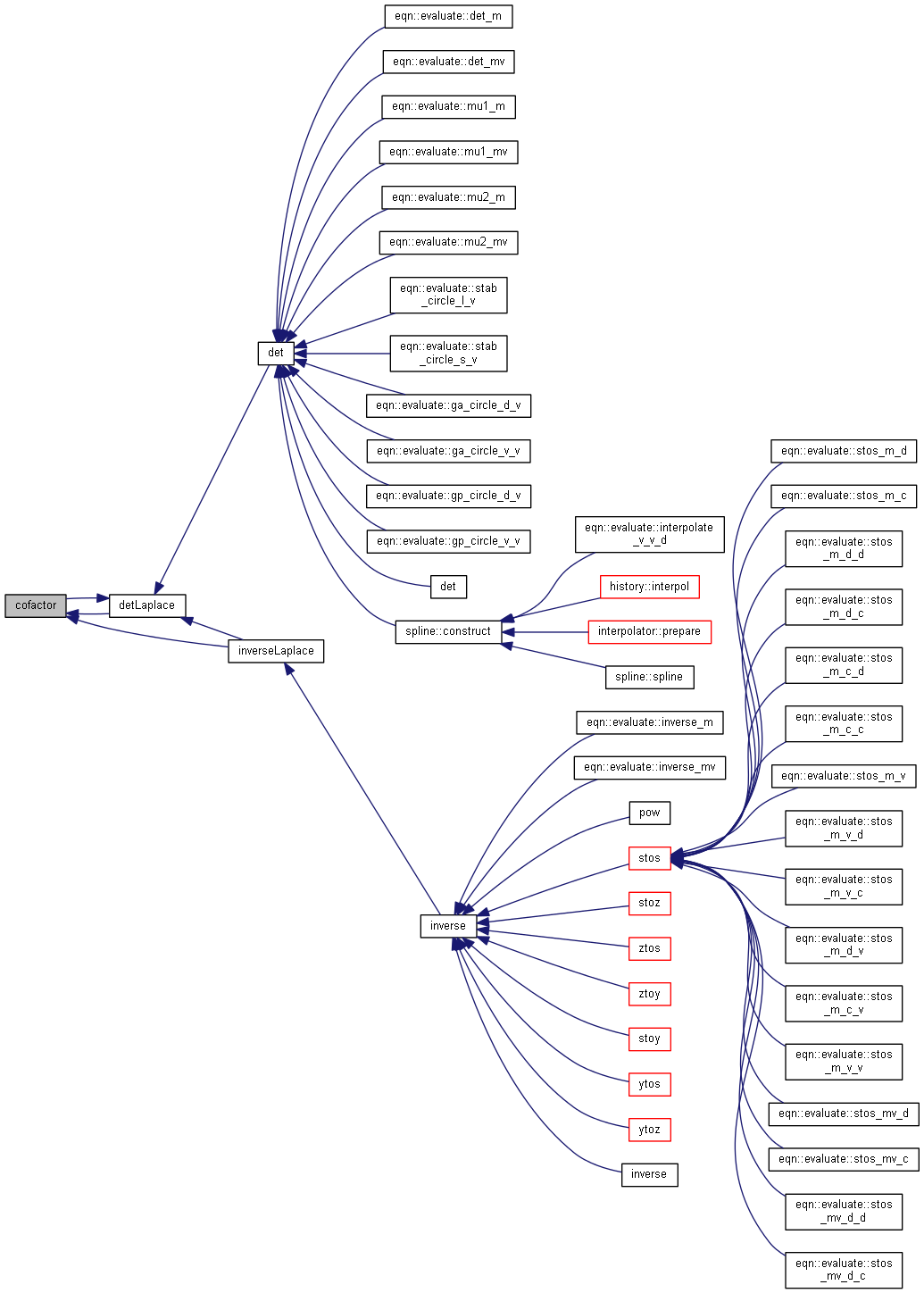
| nr_complex_t | cofactor (matrix a, int u, int v) |
| Computes the complex cofactor of the given determinant. | |
| nr_complex_t | detLaplace (matrix a) |
| Compute determinant of the given matrix using Laplace expansion. | |
| nr_complex_t | detGauss (matrix a) |
| Compute determinant Gaussian algorithm. | |
| nr_complex_t | det (matrix a) |
| Compute determinant of the given matrix. | |
| matrix | inverseLaplace (matrix a) |
| Compute inverse matrix using Laplace expansion. | |
| matrix | inverseGaussJordan (matrix a) |
| Compute inverse matrix using Gauss-Jordan elimination. | |
| matrix | inverse (matrix a) |
| Compute inverse matrix. | |
| matrix | stos (matrix s, vector zref, vector z0) |
| S params to S params. | |
| matrix | stos (matrix s, nr_complex_t zref, nr_complex_t z0) |
| S renormalization with all part identic. | |
| matrix | stos (matrix s, nr_double_t zref, nr_double_t z0) |
| S renormalization with all part identic and real. | |
| matrix | stos (matrix s, vector zref, nr_complex_t z0) |
| S renormalization (variation) | |
| matrix | stos (matrix s, nr_complex_t zref, vector z0) |
| S renormalization (variation) | |
| matrix | stoz (matrix s, vector z0) |
| Scattering parameters to impedance matrix. | |
| matrix | stoz (matrix s, nr_complex_t z0) |
| Scattering parameters to impedance matrix identic case. | |
| matrix | ztos (matrix z, vector z0) |
| Convert impedance matrix scattering parameters. | |
| matrix | ztos (matrix z, nr_complex_t z0) |
| Convert impedance matrix to scattering parameters identic case. | |
| matrix | ztoy (matrix z) |
| impedance matrix to admittance matrix. | |
| matrix | stoy (matrix s, vector z0) |
| Scattering parameters to admittance matrix. | |
| matrix | stoy (matrix s, nr_complex_t z0) |
| Convert scattering pto adminttance parameters identic case. | |
| matrix | ytos (matrix y, vector z0) |
| Admittance matrix to scattering parameters. | |
| matrix | ytos (matrix y, nr_complex_t z0) |
| Convert Admittance matrix to scattering parameters identic case. | |
| matrix | stoa (matrix s, nr_complex_t z1, nr_complex_t z2) |
| Converts chain matrix to scattering parameters. | |
| matrix | atos (matrix a, nr_complex_t z1, nr_complex_t z2) |
| Converts chain matrix to scattering parameters. | |
| matrix | stoh (matrix s, nr_complex_t z1, nr_complex_t z2) |
| Converts scattering parameters to hybrid matrix. | |
| matrix | htos (matrix h, nr_complex_t z1, nr_complex_t z2) |
| Converts hybrid matrix to scattering parameters. | |
| matrix | stog (matrix s, nr_complex_t z1, nr_complex_t z2) |
| matrix | gtos (matrix g, nr_complex_t z1, nr_complex_t z2) |
| matrix | ytoz (matrix y) |
| Convert admittance matrix to impedance matrix. | |
| matrix | cytocs (matrix cy, matrix s) |
| Admittance noise correlation matrix to S-parameter noise correlation matrix. | |
| matrix | cstocy (matrix cs, matrix y) |
| Converts S-parameter noise correlation matrix to admittance noise correlation matrix. | |
| matrix | cztocs (matrix cz, matrix s) |
| Converts impedance noise correlation matrix to S-parameter noise correlation matrix. | |
| matrix | cstocz (matrix cs, matrix z) |
| Converts S-parameter noise correlation matrix to impedance noise correlation matrix. | |
| matrix | cztocy (matrix cz, matrix y) |
| Converts impedance noise correlation matrix to admittance noise correlation matrix. | |
| matrix | cytocz (matrix cy, matrix z) |
| Converts admittance noise correlation matrix to impedance noise correlation matrix. | |
| matrix | twoport (matrix m, char in, char out) |
| Generic conversion matrix. | |
Dense matrix class implementation.
References:
[1] Power Waves and the Scattering Matrix Kurokawa, K. Microwave Theory and Techniques, IEEE Transactions on, Vol.13, Iss.2, Mar 1965 Pages: 194- 202
[2] A Rigorous Technique for Measuring the Scattering Matrix of a Multiport Device with a 2-Port Network Analyzer John C. TIPPET, Ross A. SPECIALE Microwave Theory and Techniques, IEEE Transactions on, Vol.82, Iss.5, May 1982 Pages: 661- 666
[3] Comments on "A Rigorous Techique for Measuring the Scattering Matrix of a Multiport Device with a Two-Port Network Analyzer" Dropkin, H. Microwave Theory and Techniques, IEEE Transactions on, Vol. 83, Iss.1, Jan 1983 Pages: 79 - 81
[4] Arbitrary Impedance "Accurate Measurements In Almost Any Impedance Environment" in Scropion Application note Anritsu online(2007/07/30) http://www.eu.anritsu.com/files/11410-00284B.pdf
[5] Conversions between S, Z, Y, H, ABCD, and T parameters which are valid for complex source and load impedances Frickey, D.A. Microwave Theory and Techniques, IEEE Transactions on Vol. 42, Iss. 2, Feb 1994 pages: 205 - 211 doi: 10.1109/22.275248
[6] Comments on "Conversions between S, Z, Y, h, ABCD, and T parameters which are valid for complex source and load impedances" [and reply] Marks, R.B.; Williams, D.F.; Frickey, D.A. Microwave Theory and Techniques, IEEE Transactions on, Vol.43, Iss.4, Apr 1995 Pages: 914- 915 doi: 10.1109/22.375247
[7] Wave Techniques for Noise Modeling and Measurement S. W. Wedge and D. B. Rutledge, IEEE Transactions on Microwave Theory and Techniques, vol. 40, no. 11, Nov. 1992. pages 2004-2012, doi: 10.1109/22.168757 Author copy online (2007/07/31) http://authors.library.caltech.edu/6226/01/WEDieeetmtt92.pdf
Definition in file matrix.cpp.
Computes magnitude of each matrix element.
| [in] | a | matrix |
add abs in place
a is const
Definition at line 529 of file matrix.cpp.
adjoint matrix
The function returns the adjoint complex matrix. This is also called the adjugate or transpose conjugate.
| [in] | a | Matrix to transpose |
add adjoint in place
Do not lazy and avoid conj and transpose copy
a is const
Definition at line 520 of file matrix.cpp.
Computes the argument of each matrix element.
| [in] | a | matrix |
add arg in place
a is const
Definition at line 553 of file matrix.cpp.
| matrix atos | ( | matrix | a, |
| nr_complex_t | z1 = 50.0, |
||
| nr_complex_t | z2 = 50.0 |
||
| ) |
Converts chain matrix to scattering parameters.
Converts chain matrix to scattering parameters Formulae are given by [5] and are remembered here:

Where:
![\[ \Delta =AZ_{02}+B+CZ_{01}Z_{02}-DZ_{01} \]](form_107.png)
| [in] | a | Chain matrix |
| [in] | z1 | impedance at input 1 |
| [in] | z2 | impedance at input 2 |
Definition at line 1213 of file matrix.cpp.
| nr_complex_t cofactor | ( | matrix | a, |
| int | u, | ||
| int | v | ||
| ) |
Computes the complex cofactor of the given determinant.
The cofactor is the determinant obtained by deleting the row and column of a given element of a matrix or determinant. The cofactor is preceded by a + or - sign depending of the sign of 
((u + v) & 1) is cryptic use (u + v)% 2
#ifdef 0
static?
Definition at line 648 of file matrix.cpp.
Conjugate complex matrix.
| [in] | a | Matrix to conjugate |
add conj in place
a is const
Definition at line 503 of file matrix.cpp.
Converts S-parameter noise correlation matrix to admittance noise correlation matrix.
According to [7] fig 2:
![\[ C_y=(I+Y)C_s(I+Y)^+ \]](form_118.png)
Where  is the scattering noise correlation matrix,
is the scattering noise correlation matrix,  the admittance noise correlation matrix,
the admittance noise correlation matrix,  the identity matrix and
the identity matrix and  the scattering matrix of device.
the scattering matrix of device.  is the adjoint of
is the adjoint of 
| [in] | cs | S parameter noise correlation |
| [in] | y | Admittance matrix of device |
Definition at line 1421 of file matrix.cpp.

Converts S-parameter noise correlation matrix to impedance noise correlation matrix.
According to [7] fig 2:
![\[ C_z=(I+Z)C_s(I+Z)^+ \]](form_121.png)
Where  is the scattering noise correlation matrix,
is the scattering noise correlation matrix,  the impedance noise correlation matrix,
the impedance noise correlation matrix,  the identity matrix and
the identity matrix and  the scattering matrix of device.
the scattering matrix of device.  is the adjoint of
is the adjoint of 
| [in] | cs | S parameter noise correlation |
| [in] | z | Impedance matrix of device |
Definition at line 1474 of file matrix.cpp.
Admittance noise correlation matrix to S-parameter noise correlation matrix.
Converts admittance noise correlation matrix to S-parameter noise correlation matrix. According to [7] fig 2:
![\[ C_s=\frac{1}{4}(I+S)C_y(I+S)^+ \]](form_114.png)
Where  is the scattering noise correlation matrix,
is the scattering noise correlation matrix,  the admittance noise correlation matrix,
the admittance noise correlation matrix,  the identity matrix and
the identity matrix and  the scattering matrix of device.
the scattering matrix of device.  is the adjoint of
is the adjoint of 
| [in] | cy | Admittance noise correlation |
| [in] | s | S parameter matrix of device |
Definition at line 1395 of file matrix.cpp.
Converts admittance noise correlation matrix to impedance noise correlation matrix.
According to [7] fig 2:
![\[ C_z=ZC_yZ^+ \]](form_123.png)
Where  is the impedance correlation matrix,
is the impedance correlation matrix,  the identity matrix and
the identity matrix and  the admittance noise correlation matrix.
the admittance noise correlation matrix.  is the adjoint of
is the adjoint of 
| [in] | cy | Admittance noise correlation |
| [in] | z | Impedance matrix of device |
Definition at line 1522 of file matrix.cpp.
Converts impedance noise correlation matrix to S-parameter noise correlation matrix.
According to [7] fig 2:
![\[ C_s=\frac{1}{4}(I-S)C_z(I-S) \]](form_119.png)
Where  is the scattering noise correlation matrix,
is the scattering noise correlation matrix,  the impedance noise correlation matrix,
the impedance noise correlation matrix,  the identity matrix and
the identity matrix and  the scattering matrix of device.
the scattering matrix of device.  is the adjoint of
is the adjoint of 
| [in] | cz | Impedance noise correlation |
| [in] | s | S parameter matrix of device |
Definition at line 1448 of file matrix.cpp.
Converts impedance noise correlation matrix to admittance noise correlation matrix.
According to [7] fig 2:
![\[ C_y=YC_zY^+ \]](form_122.png)
Where  is the impedance correlation matrix,
is the impedance correlation matrix,  the identity matrix and
the identity matrix and  the admittance noise correlation matrix.
the admittance noise correlation matrix.  is the adjoint of
is the adjoint of 
| [in] | cz | impedance noise correlation |
| [in] | y | Admittance matrix of device |
Definition at line 1498 of file matrix.cpp.
Computes magnitude in dB of each matrix element.
| [in] | a | matrix |
Definition at line 540 of file matrix.cpp.
| nr_complex_t det | ( | matrix | a | ) |
Compute determinant of the given matrix.
| [in] | a | matrix |
Definition at line 753 of file matrix.cpp.
| nr_complex_t detGauss | ( | matrix | a | ) |
Compute determinant Gaussian algorithm.
Compute determinant of the given matrix using the Gaussian algorithm. This means to triangulate the matrix and multiply all the diagonal elements.
| [in] | a | matrix |
static ?
a const?
Definition at line 708 of file matrix.cpp.
| nr_complex_t detLaplace | ( | matrix | a | ) |
Compute determinant of the given matrix using Laplace expansion.
The Laplace expansion of the determinant of an n by n square matrix a expresses the determinant of a as a sum of n determinants of (n-1) by (n-1) sub-matrices of a. There are 2n such expressions, one for each row and column of a.
See Wikipedia http://en.wikipedia.org/wiki/Laplace_expansion
| [in] | a | matrix |
#ifdef 0
static ?
Definition at line 677 of file matrix.cpp.
Create a diagonal matrix from a vector.
| [in] | diag | vector to write on the diagonal |
Definition at line 615 of file matrix.cpp.

| matrix eye | ( | int | rs, |
| int | cs | ||
| ) |
Create identity matrix with specified number of rows and columns.
| [in] | rs | row number |
| [in] | cs | column number |
Avoid res.get*
Use memset
rs, cs are const
Definition at line 594 of file matrix.cpp.
| matrix eye | ( | int | s | ) |
Create a square identity matrix.
| [in] | s | row or column number of square matrix |
Do not by lazy and implement it
s is const
Definition at line 607 of file matrix.cpp.
| matrix gtos | ( | matrix | g, |
| nr_complex_t | z1 = 50.0, |
||
| nr_complex_t | z2 = 50.0 |
||
| ) |
Definition at line 1346 of file matrix.cpp.
| matrix htos | ( | matrix | h, |
| nr_complex_t | z1 = 50.0, |
||
| nr_complex_t | z2 = 50.0 |
||
| ) |
Converts hybrid matrix to scattering parameters.
Formulae are given by [5] and are remembered here:

Where  is:
is:
![\[ \Delta=(Z_{01}+h_{11})(1+h_{22}Z_{02})-h_{12}h_{21}Z_{02} \]](form_112.png)
| [in] | h | hybrid matrix |
| [in] | z1 | impedance at input 1 |
| [in] | z2 | impedance at input 2 |
Definition at line 1298 of file matrix.cpp.
Imaginary part matrix.
| [in] | a | matrix |
add imag in place
a is const
Definition at line 579 of file matrix.cpp.
Compute inverse matrix.
| [in] | a | matrix to invert |
Definition at line 838 of file matrix.cpp.
Compute inverse matrix using Gauss-Jordan elimination.
Compute inverse matrix of the given matrix by Gauss-Jordan elimination.
a const?
static?
| [in] | a | matrix to invert |
Definition at line 789 of file matrix.cpp.
Compute inverse matrix using Laplace expansion.
Compute inverse matrix of the given matrix using Laplace expansion.
| [in] | a | matrix to invert |
Static?
#ifdef 0
Definition at line 770 of file matrix.cpp.
| matrix operator* | ( | matrix | a, |
| nr_complex_t | z | ||
| ) |
Matrix scaling complex version.
| [in] | a | matrix to scale |
| [in] | z | scaling complex |
Definition at line 296 of file matrix.cpp.
| matrix operator* | ( | nr_complex_t | z, |
| matrix | a | ||
| ) |
Matrix scaling complex version (different order)
| [in] | a | matrix to scale |
| [in] | z | scaling complex |
Why not a and z const
Why not inline
Definition at line 311 of file matrix.cpp.
Matrix scaling complex version.
| [in] | a | matrix to scale |
| [in] | d | scaling real |
Definition at line 321 of file matrix.cpp.
Matrix scaling real version (different order)
| [in] | a | matrix to scale |
| [in] | d | scaling real |
Why not inline?
Why not d and a const
Definition at line 336 of file matrix.cpp.
Matrix multiplication.
Dumb and not optimized matrix multiplication
| a] | first matrix |
| b] | second matrix |
Definition at line 376 of file matrix.cpp.
Matrix addition.
| a] | first matrix |
| b] | second matrix |
Definition at line 226 of file matrix.cpp.
| matrix operator+ | ( | matrix | a, |
| nr_complex_t | z | ||
| ) |
Complex scalar addition.
| [in] | a | matrix |
| [in] | z | complex to add |
Move near other +
a and z are const
Definition at line 397 of file matrix.cpp.
| matrix operator+ | ( | nr_complex_t | z, |
| matrix | a | ||
| ) |
Complex scalar addition different order.
| [in] | a | matrix |
| [in] | z | complex to add |
Move near other +
a and z are const
Why not inline
Definition at line 412 of file matrix.cpp.
Real scalar addition.
| [in] | a | matrix |
| [in] | d | real to add |
Move near other +
a and d are const
Definition at line 422 of file matrix.cpp.
Real scalar addition different order.
| [in] | a | matrix |
| [in] | d | real to add |
Move near other +
a and d are const
Why not inline
Definition at line 437 of file matrix.cpp.
Matrix subtraction.
| a] | first matrix |
| b] | second matrix |
Definition at line 257 of file matrix.cpp.
| matrix operator- | ( | matrix | a, |
| nr_complex_t | z | ||
| ) |
Complex scalar substraction.
| [in] | a | matrix |
| [in] | z | complex to add |
Move near other +
a and z are const
Why not inline
Definition at line 448 of file matrix.cpp.
| matrix operator- | ( | nr_complex_t | z, |
| matrix | a | ||
| ) |
Complex scalar substraction different order.
| [in] | a | matrix |
| [in] | z | complex to add |
Move near other +
a and z are const
Why not inline
Definition at line 459 of file matrix.cpp.
Real scalar substraction.
| [in] | a | matrix |
| [in] | z | real to add |
Move near other +
a and z are const
Why not inline
Definition at line 470 of file matrix.cpp.
Real scalar substraction different order.
| [in] | a | matrix |
| [in] | z | real to add |
Move near other +
a and z are const
Why not inline
Definition at line 481 of file matrix.cpp.
| matrix operator/ | ( | matrix | a, |
| nr_complex_t | z | ||
| ) |
Matrix scaling division by complex version.
| [in] | a | matrix to scale |
| [in] | z | scaling complex |
Definition at line 346 of file matrix.cpp.
Matrix scaling division by real version.
| [in] | a | matrix to scale |
| [in] | d | scaling real |
Definition at line 360 of file matrix.cpp.
Real part matrix.
| [in] | a | matrix |
add real in place
a is const
Definition at line 566 of file matrix.cpp.
| matrix stoa | ( | matrix | s, |
| nr_complex_t | z1 = 50.0, |
||
| nr_complex_t | z2 = 50.0 |
||
| ) |
Converts chain matrix to scattering parameters.
Converts scattering parameters to chain matrix. Formulae are given by [5] tab 1. and are remembered here:

Where:
![\[ \Delta = 2 S_{21}\sqrt{\Re\text{e}\;Z_{01}\Re\text{e}\;Z_{02}} \]](form_105.png)
| [in] | s | Scattering matrix |
| [in] | z1 | impedance at input 1 |
| [in] | z2 | impedance at input 2 |
Definition at line 1172 of file matrix.cpp.
| matrix stog | ( | matrix | s, |
| nr_complex_t | z1 = 50.0, |
||
| nr_complex_t | z2 = 50.0 |
||
| ) |
Definition at line 1322 of file matrix.cpp.
| matrix stoh | ( | matrix | s, |
| nr_complex_t | z1 = 50.0, |
||
| nr_complex_t | z2 = 50.0 |
||
| ) |
Converts scattering parameters to hybrid matrix.
Converts chain matrix to scattering parameters Formulae are given by [5] and are remembered here:

Where  is:
is:
![\[ \Delta=(1-S_{11})(Z_{02}^*+S_{22}Z_{02})+S_{12}S_{21}Z_{02} \]](form_110.png)
| [in] | s | Scattering matrix |
| [in] | z1 | impedance at input 1 |
| [in] | z2 | impedance at input 2 |
Definition at line 1260 of file matrix.cpp.
S params to S params.
Convert scattering parameters with the reference impedance 'zref' to scattering parameters with the reference impedance 'z0'.
Detail are given in [1], under equation (32)
New scatering matrix  is:
is:
![\[ S'=A^{-1}(S-\Gamma^+)(I-\Gamma S)^{-1}A^+ \]](form_80.png)
Where x^+ is the adjoint (or complex tranposate) of x, I the identity matrix and  is diagonal the matrix such as:
is diagonal the matrix such as:  and
and  the diagonal matrix such as:
the diagonal matrix such as:
![\[ A_i = \frac{(1-r_i^*)\sqrt{|1-r_ir_i^*|}}{|1-r_i|} \]](form_83.png)
Where  is the complex conjugate of
is the complex conjugate of  and
and  is wave reflexion coefficient of
is wave reflexion coefficient of  with respect to
with respect to  (where
(where  is the new impedance and
is the new impedance and  is the old impedance), ie:
is the old impedance), ie:
![\[ r_i = \frac{Z_i'-Z_i}{Z_i'-Z_i^*} \]](form_90.png)
| [in] | s | original S matrix |
| [in] | zref | original reference impedance |
| [in] | z0 | new reference impedance |
Correct documentation about standing waves [1-4]
Implement Speciale implementation [2-3] if applicable
Definition at line 881 of file matrix.cpp.

| matrix stos | ( | matrix | s, |
| nr_complex_t | zref, | ||
| nr_complex_t | z0 = 50.0 |
||
| ) |
S renormalization with all part identic.
| [in] | s | original S matrix |
| [in] | zref | original reference impedance |
| [in] | z0 | new reference impedance |
Definition at line 901 of file matrix.cpp.
S renormalization with all part identic and real.
| [in] | s | original S matrix |
| [in] | zref | original reference impedance |
| [in] | z0 | new reference impedance |
Definition at line 914 of file matrix.cpp.
| matrix stos | ( | matrix | s, |
| vector | zref, | ||
| nr_complex_t | z0 = 50.0 |
||
| ) |
S renormalization (variation)
| [in] | s | original S matrix |
| [in] | zref | original reference impedance |
| [in] | z0 | new reference impedance |
Definition at line 926 of file matrix.cpp.
| matrix stos | ( | matrix | s, |
| nr_complex_t | zref, | ||
| vector | z0 | ||
| ) |
S renormalization (variation)
| [in] | s | original S matrix |
| [in] | zref | original reference impedance |
| [in] | z0 | new reference impedance |
Why not inline
s, zref and z0 const
Definition at line 938 of file matrix.cpp.
Scattering parameters to admittance matrix.
Convert scattering parameters to admittance matrix. According to [1] eq (19):
![\[ Z=F^{-1} (I- S)^{-1} (SG + G^+) F \]](form_91.png)
Where  is the scattering matrix,
is the scattering matrix,  is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:

Using the well know formula  , we derivate:
, we derivate:
![\[ Y=F^{-1} (SG+G^+)^{-1} (I-S) F \]](form_101.png)
| [in] | s | Scattering matrix |
| [in] | z0 | Normalisation impedance |
 in
in  because we compute
because we compute  and therefore
and therefore  will simplify.
will simplify. Definition at line 1073 of file matrix.cpp.

| matrix stoy | ( | matrix | s, |
| nr_complex_t | z0 = 50.0 |
||
| ) |
Convert scattering pto adminttance parameters identic case.
| [in] | S | Scattering matrix |
| [in] | z0 | Normalisation impedance |
Why not inline
s and z0 const
Definition at line 1092 of file matrix.cpp.
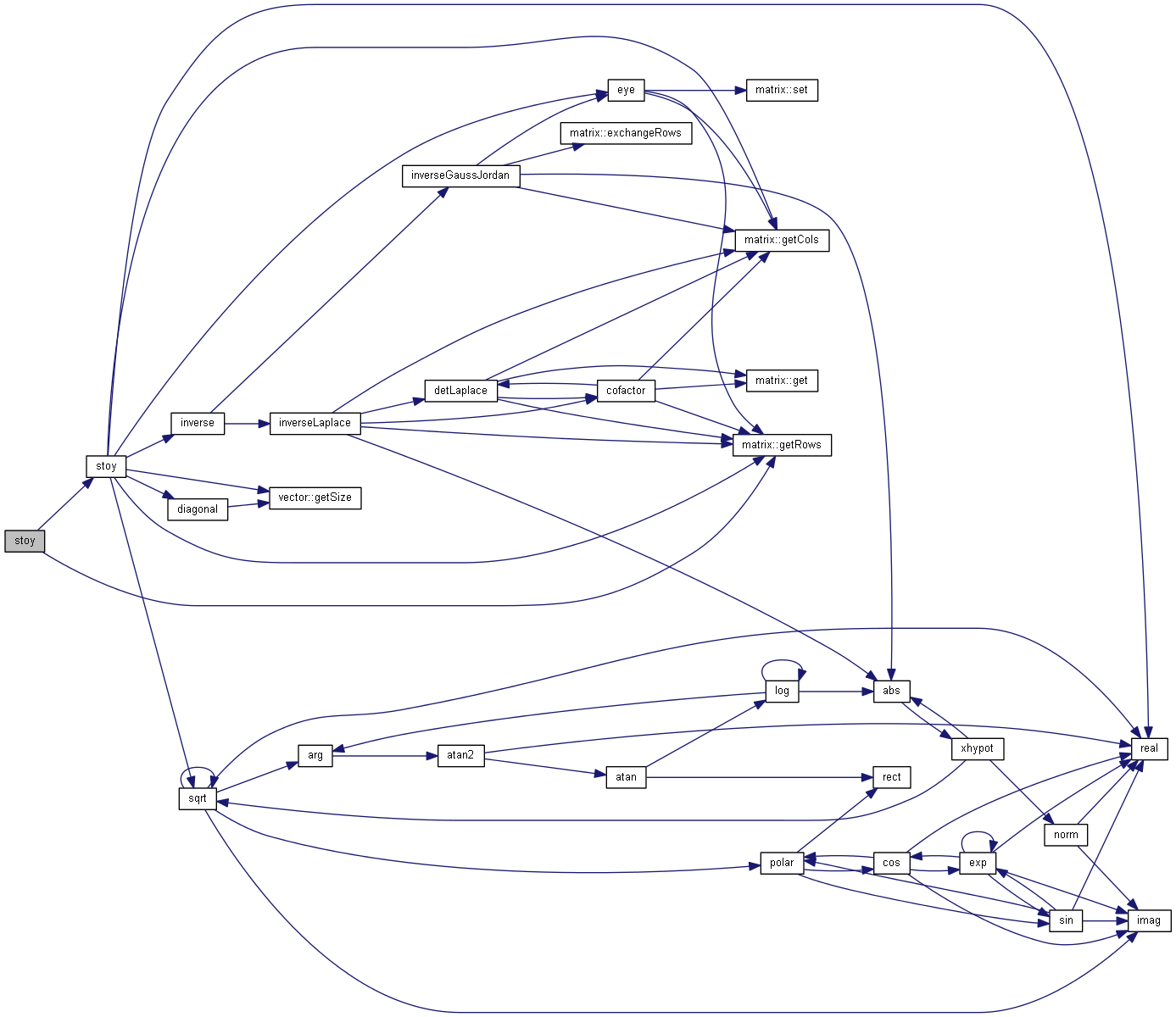
Scattering parameters to impedance matrix.
Convert scattering parameters to impedance matrix. According to [1] eq (19):
![\[ Z=F^{-1} (I- S)^{-1} (SG + G^+) F \]](form_91.png)
Where  is the scattering matrix,
is the scattering matrix,  is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:

| [in] | s | Scattering matrix |
| [in] | z0 | Normalisation impedance |
 in
in  because we compute
because we compute  and therefore
and therefore  will simplify.
will simplify. Definition at line 964 of file matrix.cpp.
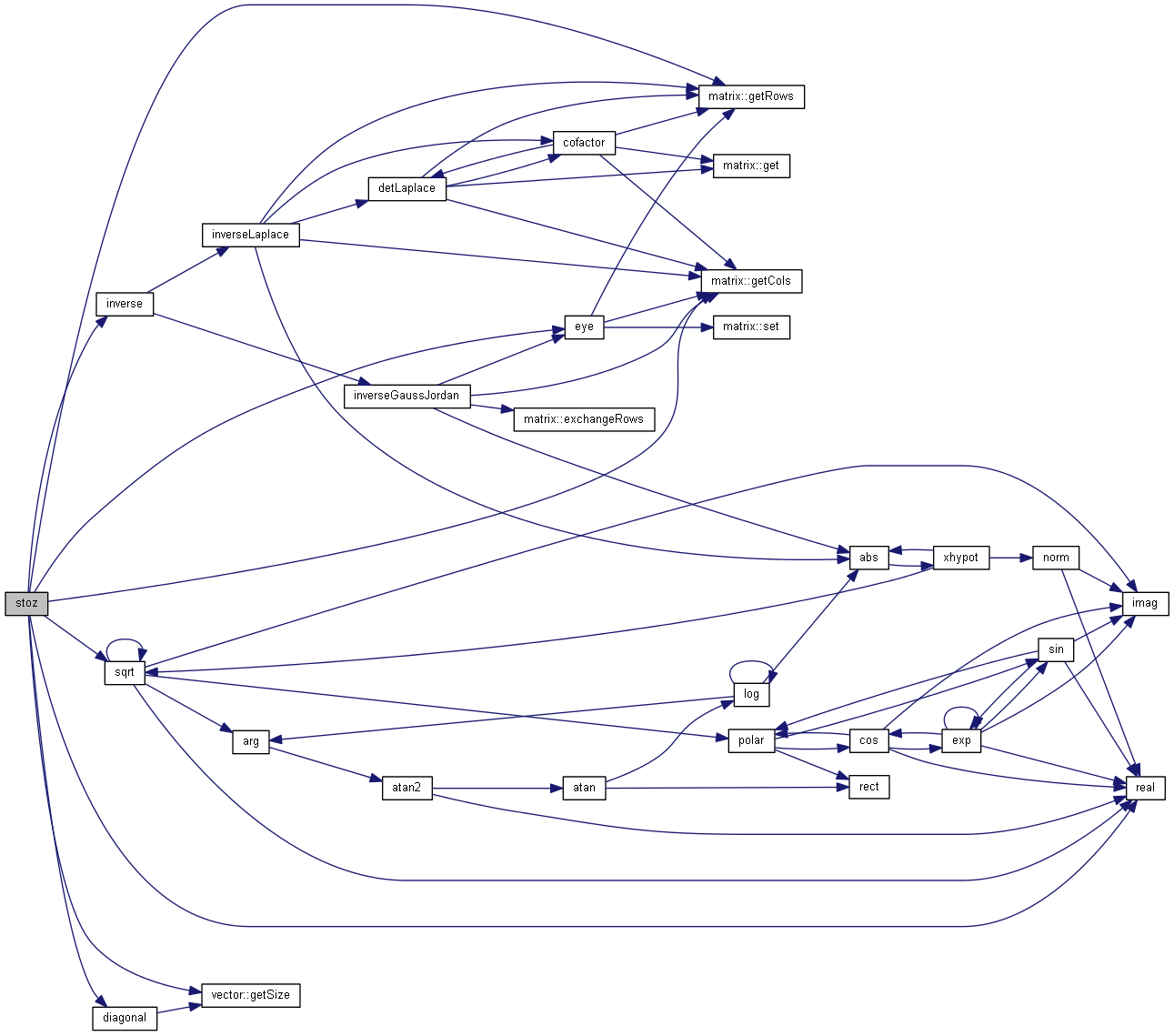
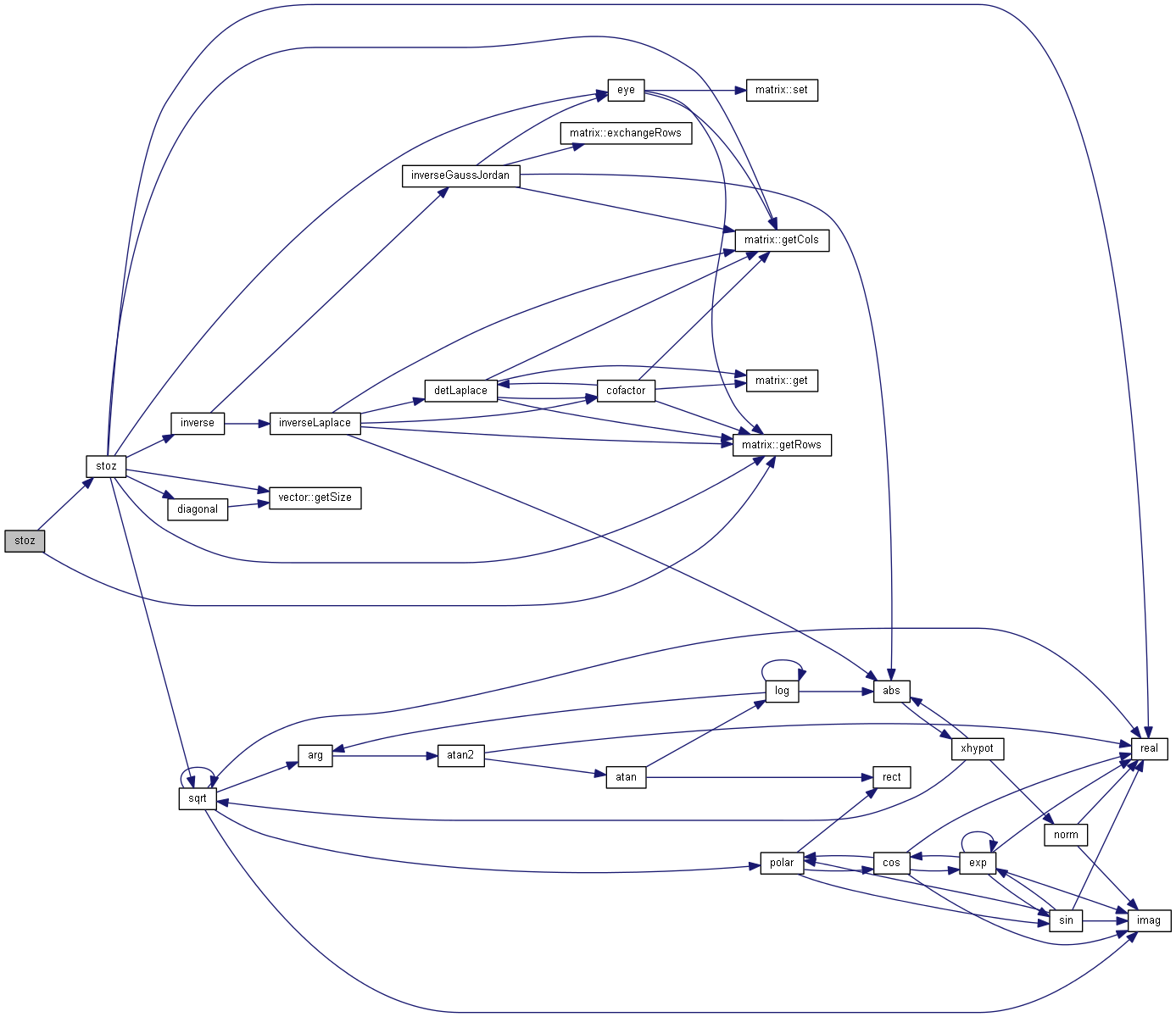
| matrix stoz | ( | matrix | s, |
| nr_complex_t | z0 = 50.0 |
||
| ) |
Scattering parameters to impedance matrix identic case.
| [in] | s | Scattering matrix |
| [in] | z0 | Normalisation impedance |
Why not inline?
s and z0 const?
Definition at line 983 of file matrix.cpp.
Matrix transposition.
| [in] | a | Matrix to transpose |
add transpose in place
a is const
Definition at line 490 of file matrix.cpp.
Generic conversion matrix.
This function converts 2x2 matrices from any of the matrix forms Y, Z, H, G and A to any other. Also converts S<->(A, T, H, Y and Z) matrices. Convertion assumed:
Y->Y, Y->Z, Y->H, Y->G, Y->A, Y->S, Z->Y, Z->Z, Z->H, Z->G, Z->A, Z->S, H->Y, H->Z, H->H, H->G, H->A, H->S, G->Y, G->Z, G->H, G->G, G->A, G->S, A->Y, A->Z, A->H, A->G, A->A, A->S, S->Y, S->Z, S->H, S->G, S->A, S->S, S->T,T->T,T->S
| [in] | m | base matrix |
| [in] | in | matrix |
| [in] | out | matrix |
Definition at line 1585 of file matrix.cpp.
Admittance matrix to scattering parameters.
Convert admittance matrix to scattering parameters. Using the same methodology as [1] eq (16-19), but writing (16) as  , ie
, ie
![\[ S=F(I-G^+Y)(I-GY)^{-1}F^{-1} \]](form_103.png)
Where  is the scattering matrix,
is the scattering matrix,  is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:

Using the well know formula  , we derivate:
, we derivate:
![\[ Y=F^{-1} (SG+G^+)^{-1} (I-S) F \]](form_101.png)
| [in] | y | admittance matrix |
| [in] | z0 | Normalisation impedance |
 in
in  because we compute
because we compute  and therefore
and therefore  will simplify.
will simplify. Definition at line 1124 of file matrix.cpp.
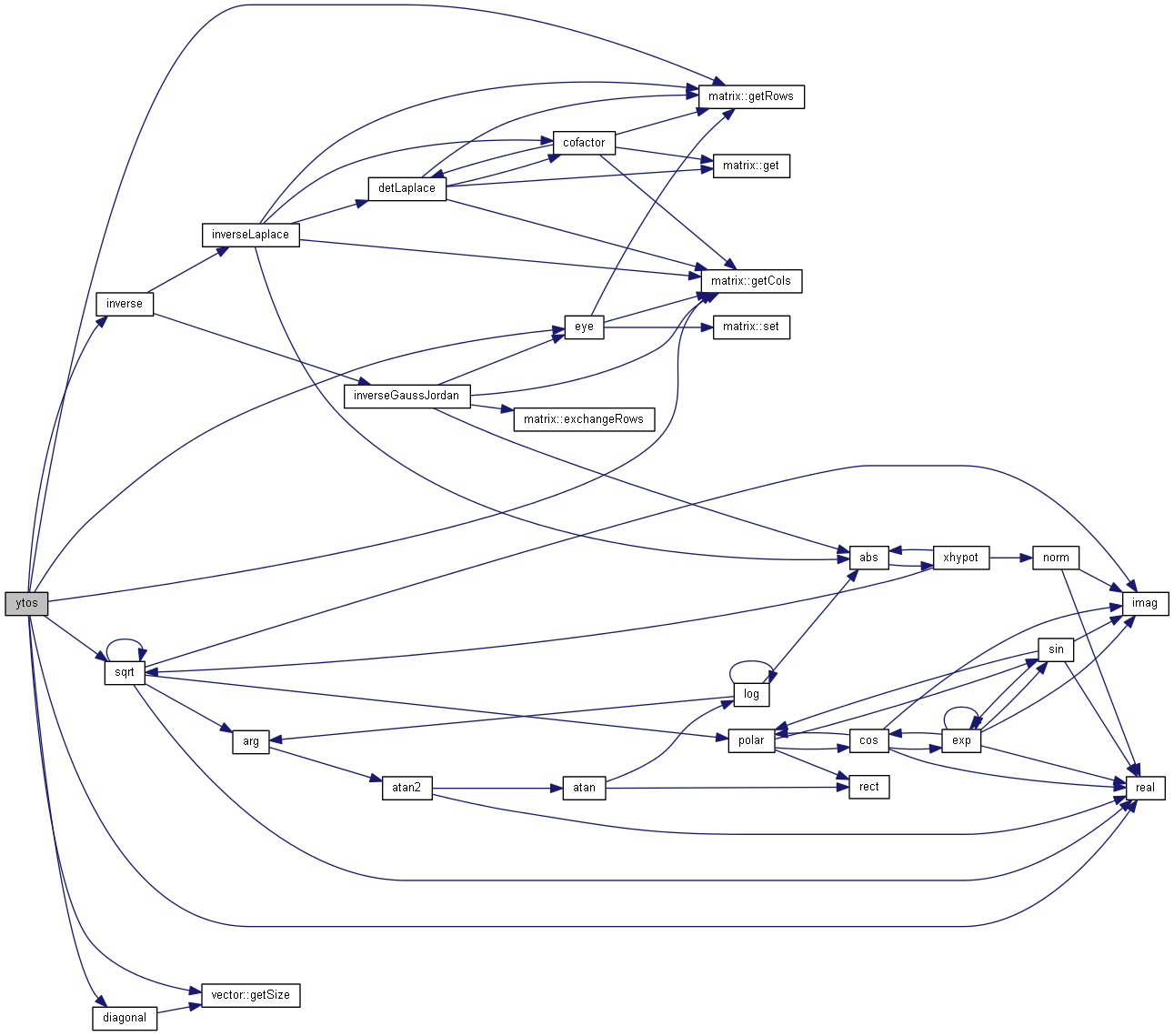
| matrix ytos | ( | matrix | y, |
| nr_complex_t | z0 = 50.0 |
||
| ) |
Convert Admittance matrix to scattering parameters identic case.
| [in] | y | Admittance matrix |
| [in] | z0 | Normalisation impedance |
Why not inline
y and z0 const
Definition at line 1142 of file matrix.cpp.
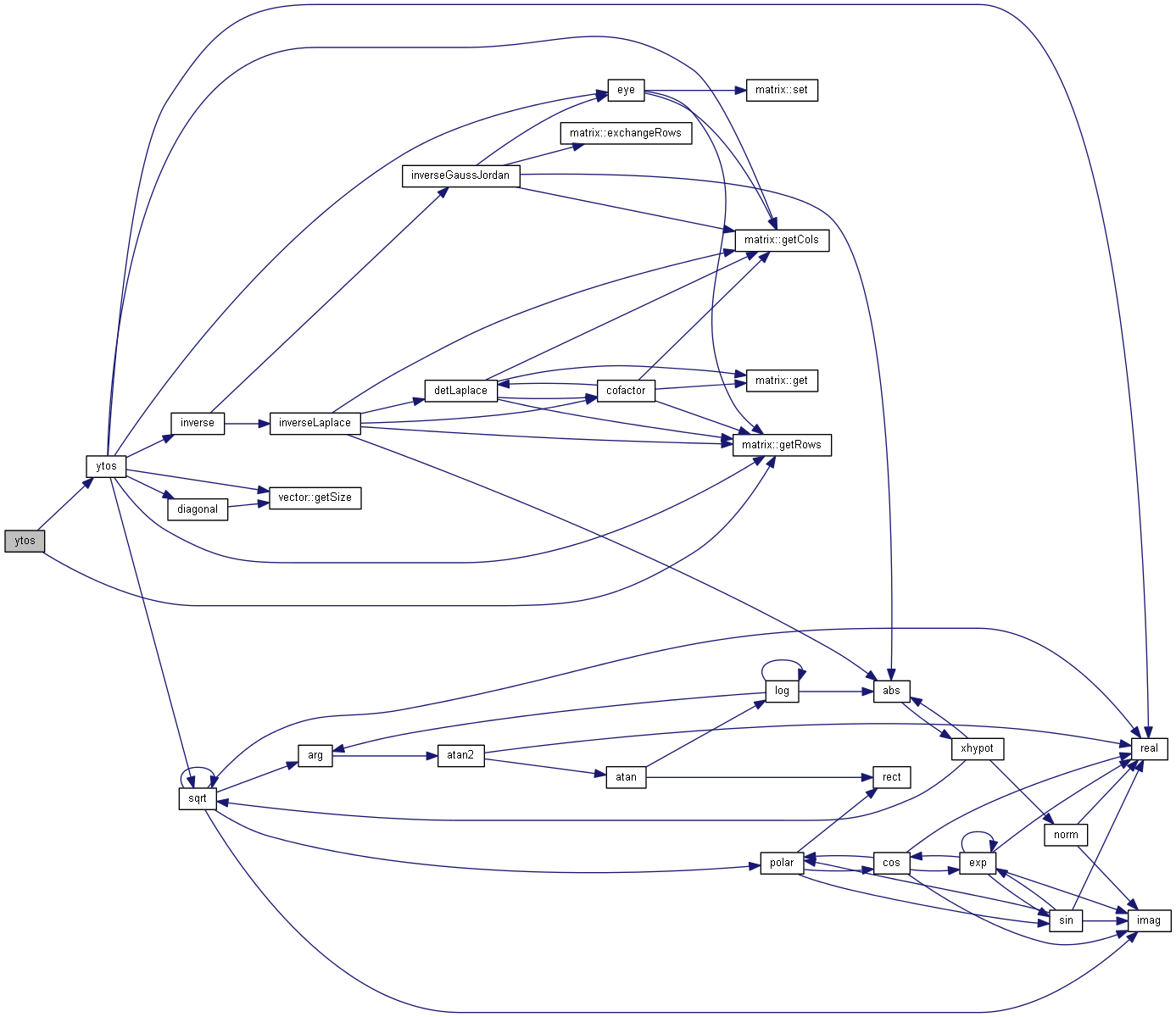
Convert admittance matrix to impedance matrix.
Convert  matrix to
matrix to  matrix using well known relation
matrix using well known relation 
| [in] | y | admittance matrix |
Definition at line 1371 of file matrix.cpp.
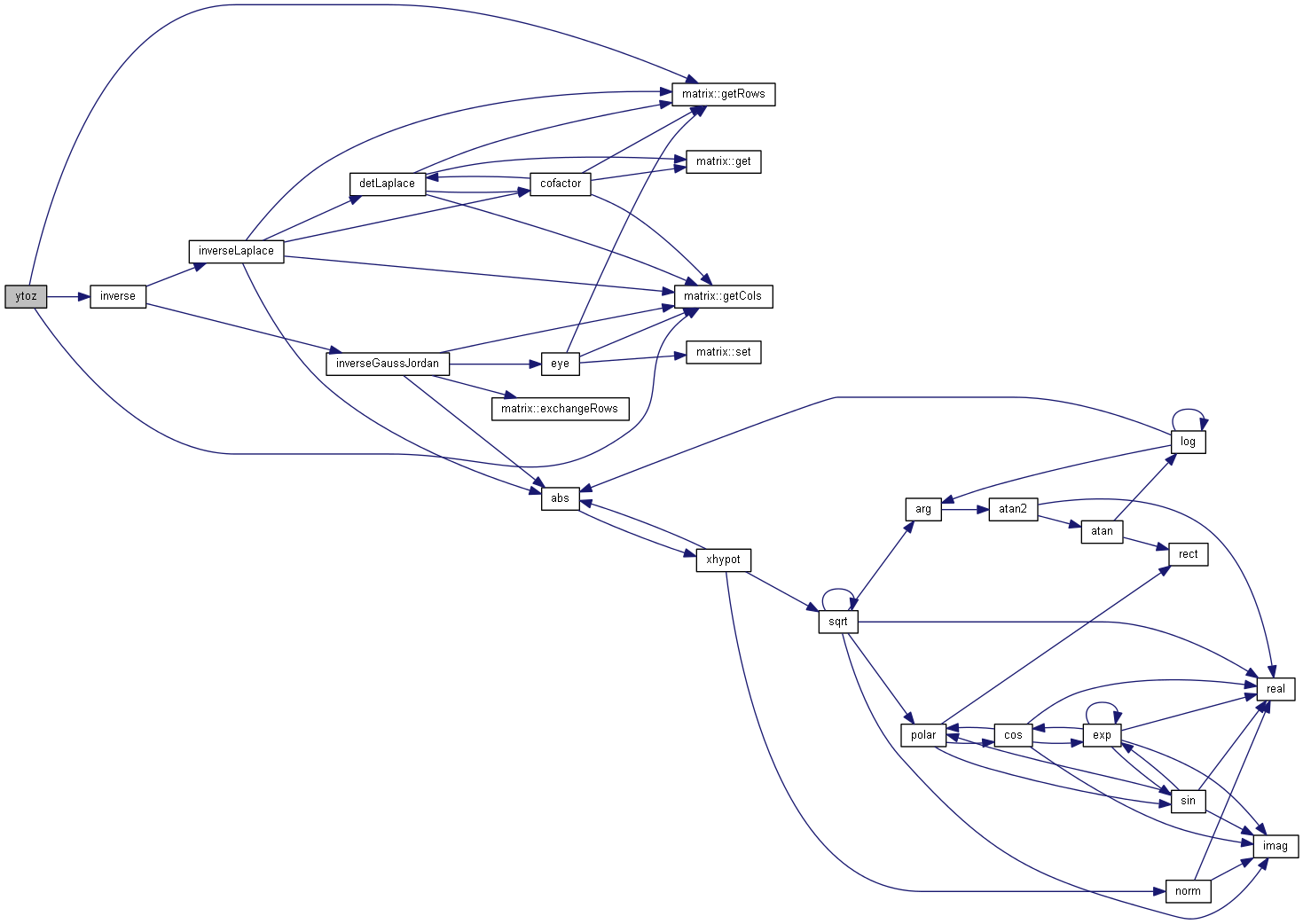
Convert impedance matrix scattering parameters.
Convert scattering parameters to impedance matrix. According to [1] eq (18):
![\[ S=F(Z-G^+)(Z+G)^{-1} F^{-1} \]](form_97.png)
Where  is the scattering matrix,
is the scattering matrix,  is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:
is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:

| [in] | Z | Impedance matrix |
| [in] | z0 | Normalisation impedance |
 in
in  because we compute
because we compute  and therefore
and therefore  will simplify.
will simplify. Definition at line 1009 of file matrix.cpp.
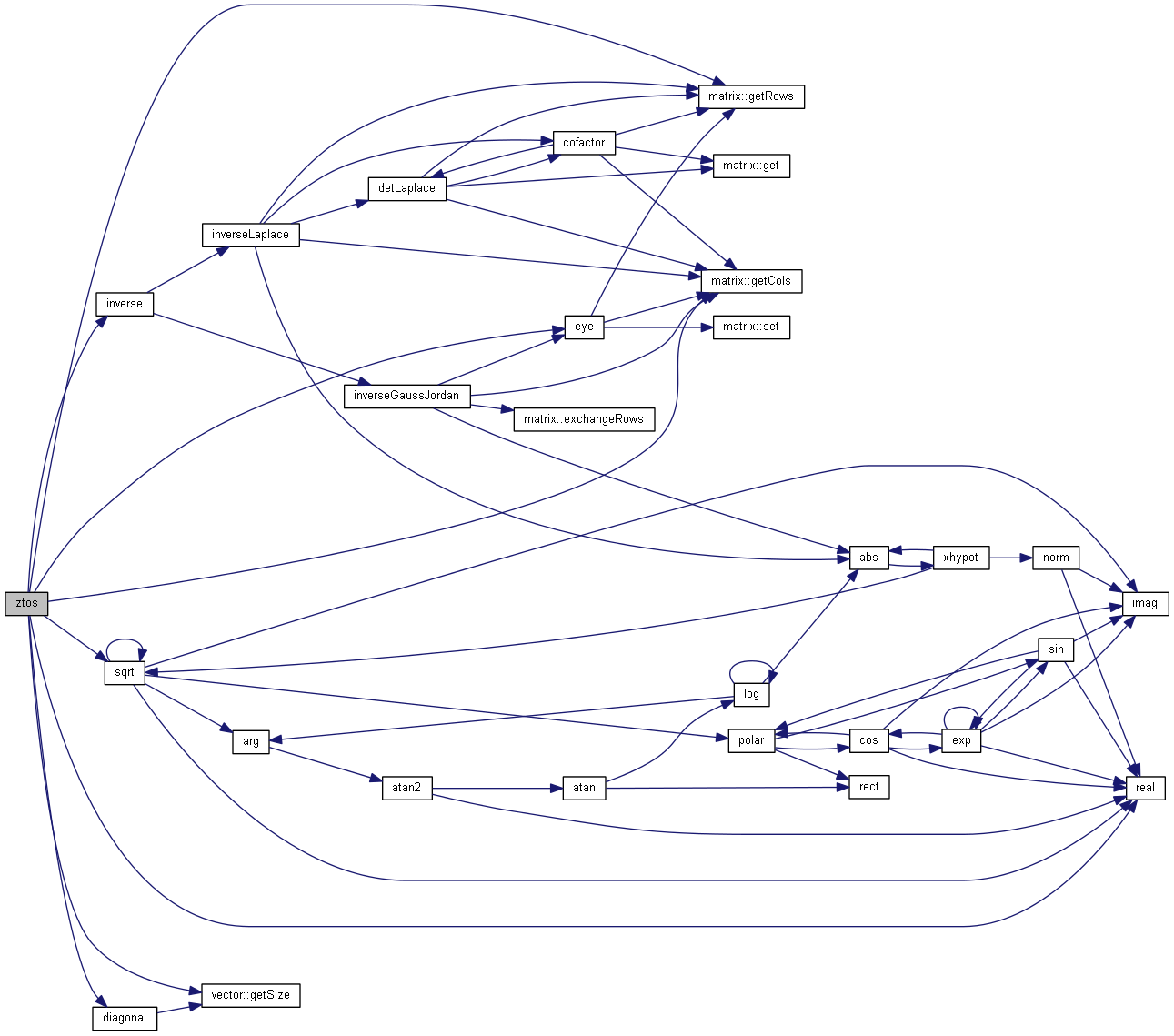
| matrix ztos | ( | matrix | z, |
| nr_complex_t | z0 = 50.0 |
||
| ) |
Convert impedance matrix to scattering parameters identic case.
| [in] | Z | Impedance matrix |
| [in] | z0 | Normalisation impedance |
Why not inline
z and z0 const
Definition at line 1028 of file matrix.cpp.
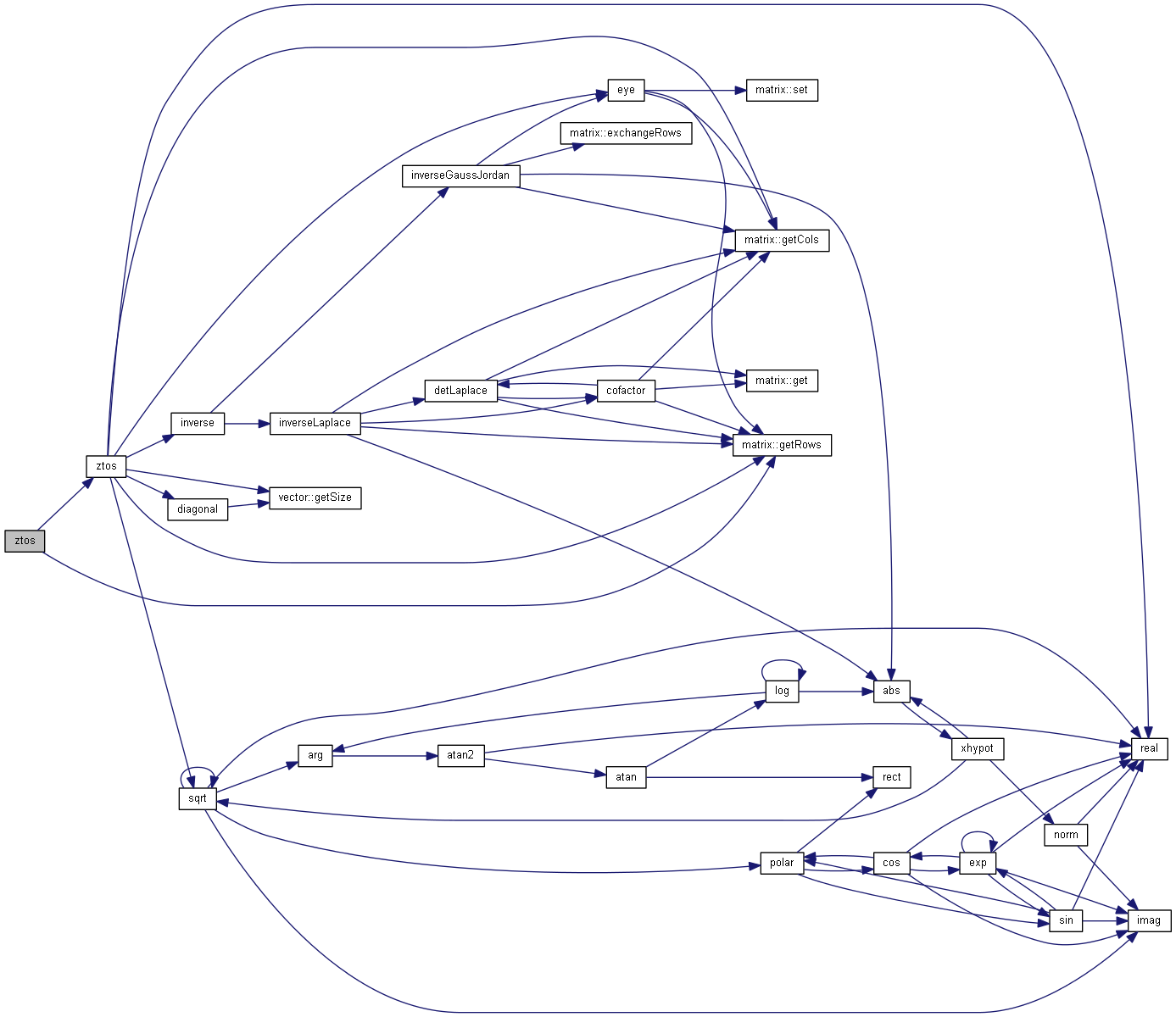
impedance matrix to admittance matrix.
Convert impedance matrix to admittance matrix. By definition 
| [in] | z | impedance matrix |
Why not inline
z const
Definition at line 1041 of file matrix.cpp.
 1.8.2
1.8.2