My Project  0.0.16
QUCS Mapping
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Pages
Typedefs | Functions
complex.h File Reference
#include "real.h"
#include "cmplx.h"
Include dependency graph for complex.h:
This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Typedefs

typedef cmplx nr_complex_t
 

Functions

nr_complex_t rect (const nr_double_t x, const nr_double_t y=0.0)
 Construct a complex number using rectangular notation.
 
nr_complex_t acos (const nr_complex_t)
 Compute complex arc cosinus.
 
nr_complex_t acosh (const nr_complex_t)
 Compute complex argument hyperbolic cosinus.
 
nr_complex_t asin (const nr_complex_t)
 Compute complex arc sinus.
 
nr_complex_t asinh (const nr_complex_t)
 Compute complex argument hyperbolic sinus.
 
nr_complex_t atan (const nr_complex_t)
 Compute complex arc tangent.
 
nr_complex_t atanh (const nr_complex_t)
 Compute complex argument hyperbolic tangent.
 
nr_complex_t atan2 (const nr_complex_t, const nr_complex_t)
 Compute complex arc tangent fortran like function.
 
nr_complex_t cos (const nr_complex_t)
 Compute complex cosinus.
 
nr_complex_t cosh (const nr_complex_t)
 Compute complex hyperbolic cosinus.
 
nr_complex_t exp (const nr_complex_t)
 Compute complex exponential.
 
nr_complex_t fmod (const nr_complex_t x, const nr_complex_t y)
 Complex fmod Apply fmod to the complex z.
 
nr_complex_t fmod (const nr_complex_t x, const nr_double_t y)
 Complex fmod (double version) Apply fmod to the complex z.
 
nr_complex_t fmod (const nr_double_t x, const nr_complex_t y)
 Complex fmod (double version) Apply fmod to the complex z.
 
nr_complex_t log (const nr_complex_t)
 Compute principal value of natural logarithm of z.
 
nr_complex_t log10 (const nr_complex_t)
 Compute principal value of decimal logarithm of z.
 
nr_complex_t log2 (const nr_complex_t)
 Compute principal value of binary logarithm of z.
 
nr_double_t norm (const nr_complex_t)
 Compute euclidian norm of complex number.
 
nr_complex_t polar (const nr_double_t mag, const nr_double_t ang=0.0)
 Construct a complex number using polar notation.
 
nr_complex_t polar (const nr_complex_t a, const nr_complex_t p)
 Extension of polar construction to complex.
 
nr_complex_t polar (const nr_double_t a, const nr_complex_t p)
 
nr_complex_t polar (const nr_complex_t a, const nr_double_t p=0.0)
 
nr_complex_t pow (const nr_complex_t, const nr_double_t)
 Compute power function with real exponent.
 
nr_complex_t pow (const nr_double_t, const nr_complex_t)
 Compute power function with complex exponent but real mantisse.
 
nr_complex_t pow (const nr_complex_t, const nr_complex_t)
 Compute complex power function.
 
nr_complex_t sin (const nr_complex_t)
 Compute complex sinus.
 
nr_complex_t sinh (const nr_complex_t)
 Compute complex hyperbolic sinus.
 
nr_complex_t sqrt (const nr_complex_t)
 Compute principal value of square root.
 
nr_complex_t tan (const nr_complex_t)
 Compute complex tangent.
 
nr_complex_t tanh (const nr_complex_t)
 Compute complex hyperbolic tangent.
 
nr_double_t dB (const nr_complex_t)
 Magnitude in dB.
 
nr_complex_t limexp (const nr_complex_t)
 Compute limited complex exponential.
 
nr_complex_t cot (const nr_complex_t)
 Compute complex cotangent.
 
nr_complex_t acot (const nr_complex_t)
 Compute complex arc cotangent.
 
nr_complex_t asech (const nr_complex_t)
 Compute complex argument hyperbolic secant.
 
nr_complex_t coth (const nr_complex_t)
 Compute complex hyperbolic cotangent.
 
nr_complex_t acoth (const nr_complex_t)
 Compute complex argument hyperbolic cotangent.
 
nr_complex_t ztor (const nr_complex_t, const nr_complex_t zref=50.0)
 Converts impedance to reflexion coefficient.
 
nr_complex_t rtoz (const nr_complex_t, const nr_complex_t zref=50.0)
 Converts reflexion coefficient to impedance.
 
nr_complex_t ytor (const nr_complex_t, const nr_complex_t zref=50.0)
 Converts admittance to reflexion coefficient.
 
nr_complex_t rtoy (const nr_complex_t, const nr_complex_t zref=50.0)
 Converts reflexion coefficient to admittance.
 
nr_complex_t signum (const nr_complex_t)
 complex signum function
 
nr_complex_t sign (const nr_complex_t)
 complex sign function
 
nr_complex_t sinc (const nr_complex_t)
 Cardinal sinus.
 
nr_double_t xhypot (const nr_complex_t, const nr_complex_t)
 Euclidean distance function for complex argument.
 
nr_double_t xhypot (const nr_double_t, const nr_complex_t)
 Euclidean distance function for a double b complex.
 
nr_double_t xhypot (const nr_complex_t, const nr_double_t)
 Euclidean distance function for b double a complex.
 
nr_complex_t floor (const nr_complex_t)
 Complex floor.
 
nr_complex_t ceil (const nr_complex_t)
 Complex ceil Ceil is the smallest integral value not less than argument Apply ceil to real and imaginary part.
 
nr_complex_t fix (const nr_complex_t)
 Complex ceil.
 
nr_complex_t trunc (const nr_complex_t)
 Complex trunc.
 
nr_complex_t round (const nr_complex_t)
 Complex round round is the nearest integral value Apply round to real and imaginary part.
 
nr_complex_t sqr (const nr_complex_t)
 Square of complex number.
 
nr_complex_t step (const nr_complex_t)
 Heaviside step function for complex number.
 
nr_complex_t jn (const int, const nr_complex_t)
 Bessel function of first kind.
 
nr_complex_t yn (const int, const nr_complex_t)
 Bessel function of second kind.
 
nr_complex_t i0 (const nr_complex_t)
 Modified Bessel function of first kind.
 
nr_complex_t erf (const nr_complex_t)
 Error function.
 
nr_complex_t erfc (const nr_complex_t)
 Complementart error function.
 
nr_complex_t erfinv (const nr_complex_t)
 Inverse of error function.
 
nr_complex_t erfcinv (const nr_complex_t)
 Inverse of complementart error function.
 
nr_complex_t operator% (const nr_complex_t, const nr_complex_t)
 Modulo.
 
nr_complex_t operator% (const nr_complex_t, const nr_double_t)
 Modulo.
 
nr_complex_t operator% (const nr_double_t, const nr_complex_t)
 Modulo.
 
bool operator== (const nr_complex_t, const nr_complex_t)
 Equality of two complex.
 
bool operator!= (const nr_complex_t, const nr_complex_t)
 Inequality of two complex.
 
bool operator>= (const nr_complex_t, const nr_complex_t)
 Superior of equal.
 
bool operator<= (const nr_complex_t, const nr_complex_t)
 Inferior of equal.
 
bool operator> (const nr_complex_t, const nr_complex_t)
 Superior.
 
bool operator< (const nr_complex_t, const nr_complex_t)
 Inferior.
 

Typedef Documentation

typedef cmplx nr_complex_t

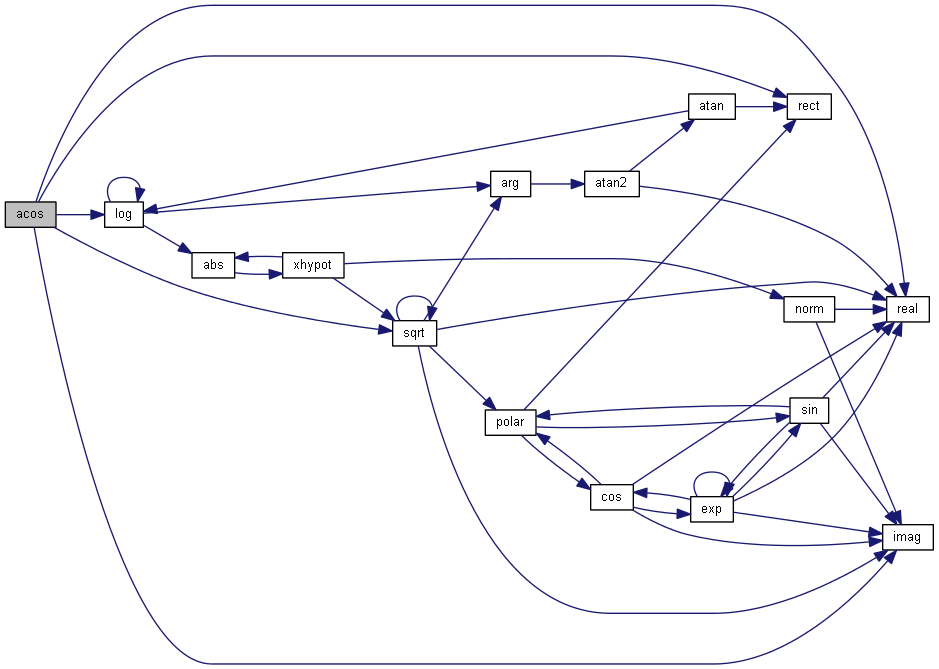
Definition at line 32 of file complex.h.

Function Documentation

nr_complex_t acos ( const nr_complex_t  z)

Compute complex arc cosinus.

Parameters
[in]zcomplex arc
Returns
arc cosinus of z

Definition at line 113 of file complex.cpp.

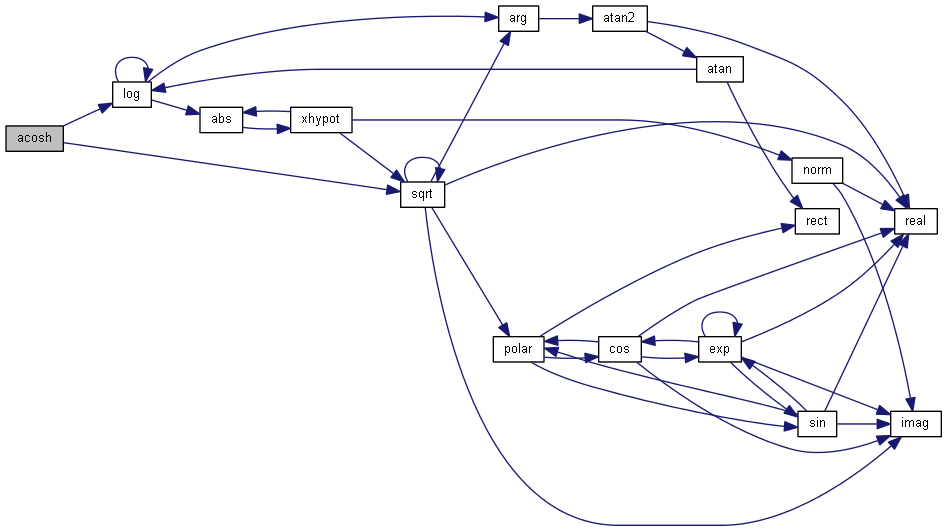
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t acosh ( const nr_complex_t  z)

Compute complex argument hyperbolic cosinus.

Parameters
[in]zcomplex arc
Returns
argument hyperbolic cosinus of z

Definition at line 145 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t acot ( const nr_complex_t  z)

Compute complex arc cotangent.

Parameters
[in]zcomplex arc
Returns
arc cotangent of z

Definition at line 414 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t acoth ( const nr_complex_t  z)

Compute complex argument hyperbolic cotangent.

Parameters
[in]zcomplex arc
Returns
argument hyperbolic cotangent of z

Definition at line 444 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t asech ( const nr_complex_t  z)

Compute complex argument hyperbolic secant.

Parameters
[in]zcomplex arc
Returns
argument hyperbolic secant of z
Todo:
for symetry reason implement sech

Definition at line 424 of file complex.cpp.

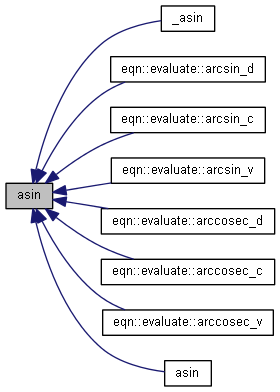
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t asin ( const nr_complex_t  z)

Compute complex arc sinus.

Parameters
[in]zcomplex arc
Returns
arc sinus of z

Definition at line 260 of file complex.cpp.

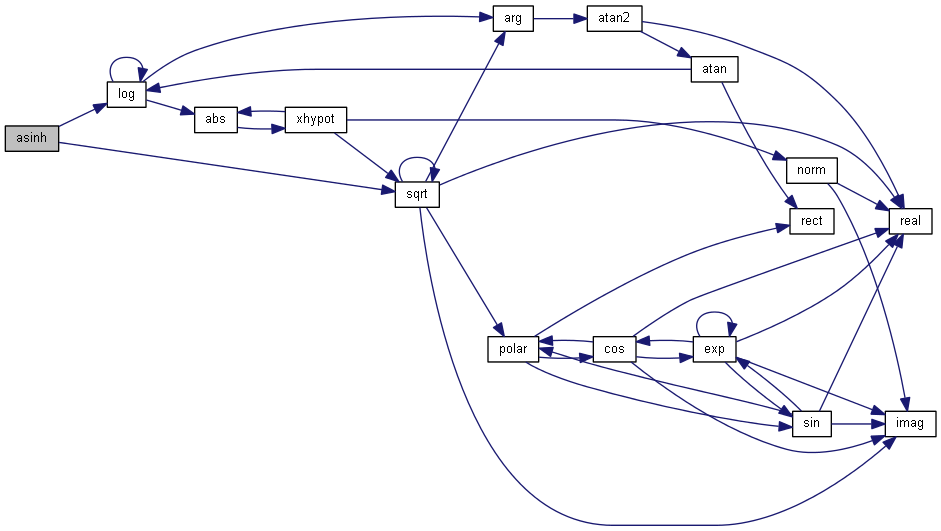
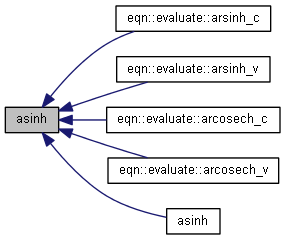
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t asinh ( const nr_complex_t  z)

Compute complex argument hyperbolic sinus.

Parameters
[in]zcomplex arc
Returns
argument hyperbolic sinus of z

Definition at line 286 of file complex.cpp.

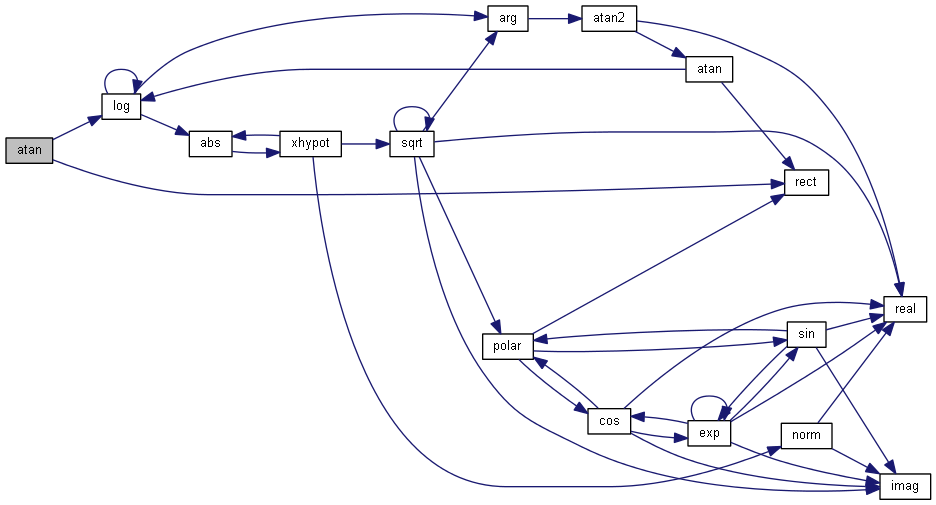
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t atan ( const nr_complex_t  z)

Compute complex arc tangent.

Parameters
[in]zcomplex arc
Returns
arc tangent of z

Definition at line 354 of file complex.cpp.

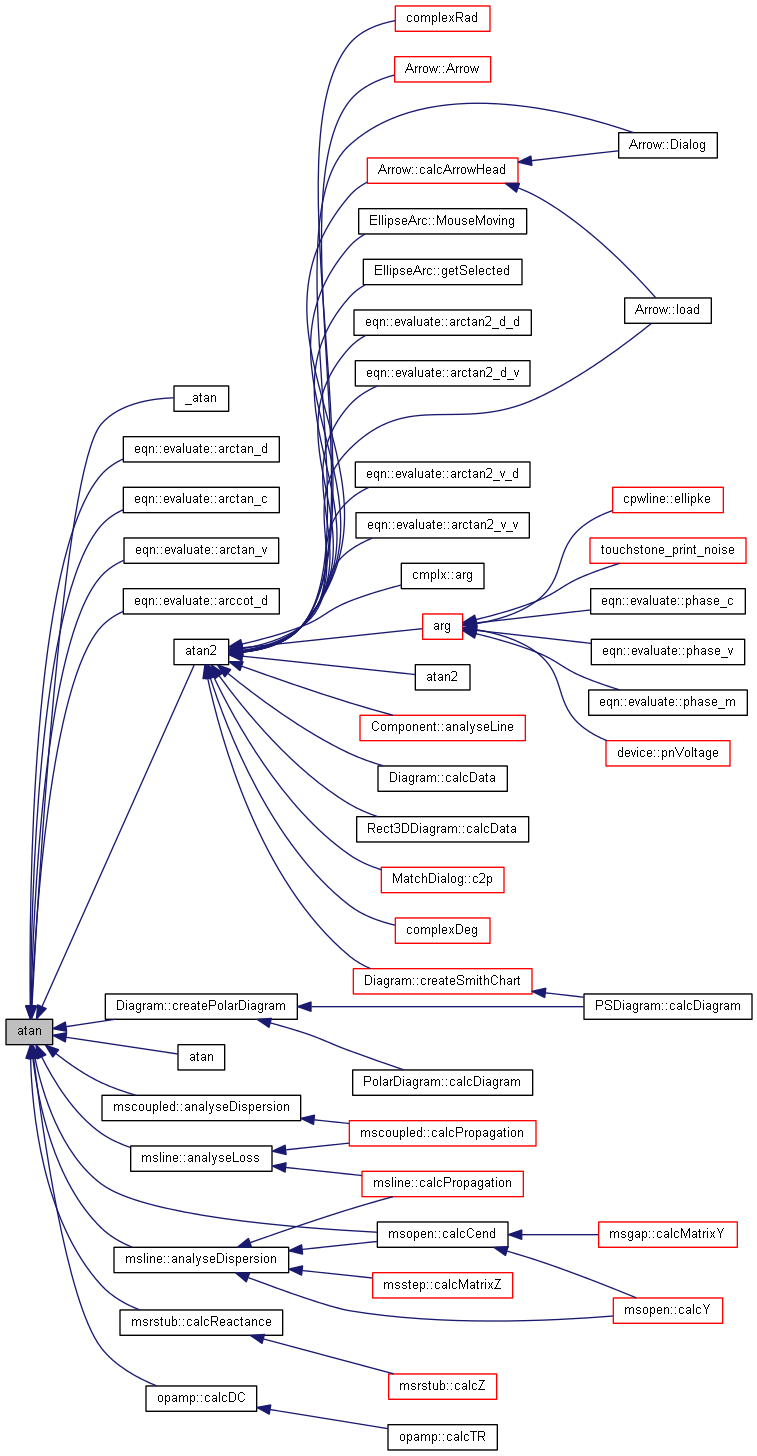
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t atan2 ( const nr_complex_t  y,
const nr_complex_t  x 
)

Compute complex arc tangent fortran like function.

atan2 is a two-argument function that computes the arc tangent of y / x given y and x, but with a range of $(-\pi;\pi]$

Parameters
[in]zcomplex angle
Returns
arc tangent of z

Definition at line 368 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t atanh ( const nr_complex_t  z)

Compute complex argument hyperbolic tangent.

Parameters
[in]zcomplex arc
Returns
argument hyperbolic tangent of z

Definition at line 393 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t ceil ( const nr_complex_t  z)

Complex ceil Ceil is the smallest integral value not less than argument Apply ceil to real and imaginary part.

Parameters
[in]zcomplex number
Returns
ceilled complex number
Todo:
Why not inline?

Definition at line 639 of file complex.cpp.

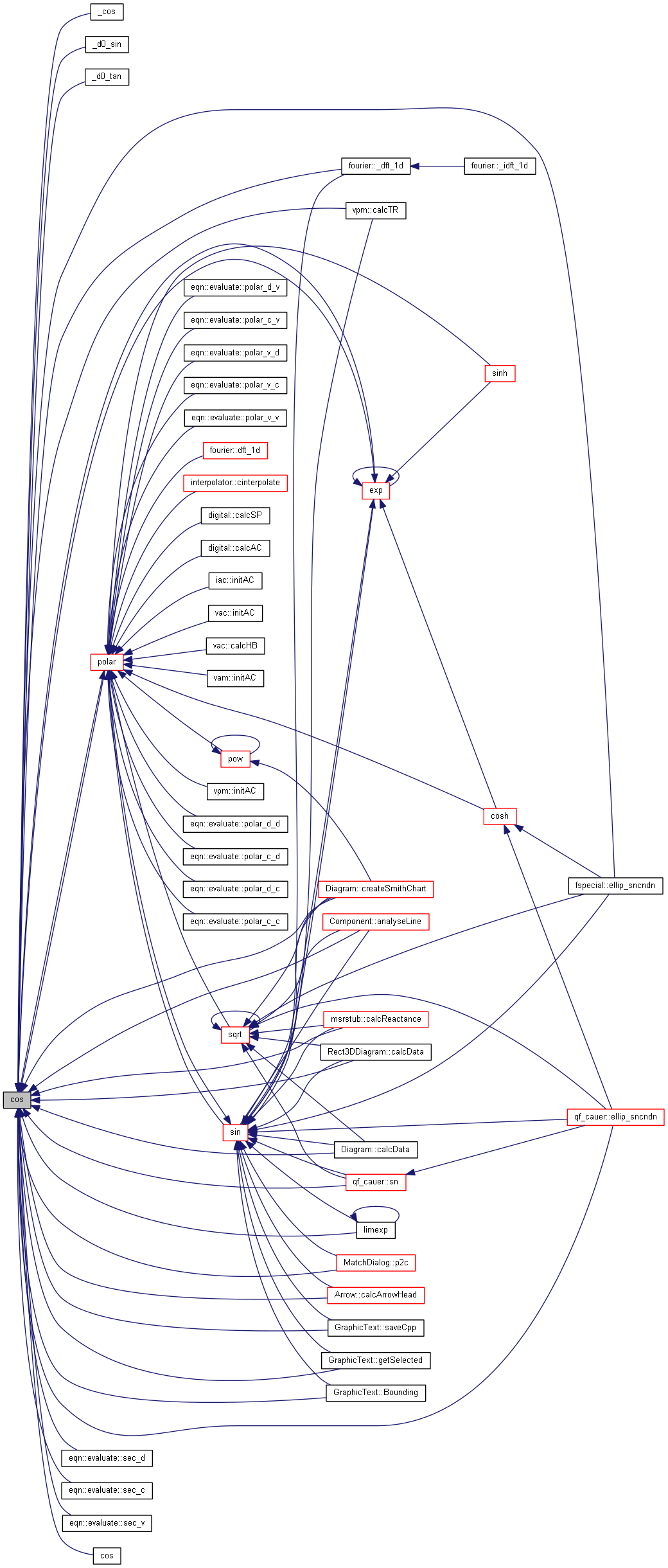
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t cos ( const nr_complex_t  z)

Compute complex cosinus.

Parameters
[in]zcomplex angle
Returns
cosinus of z

Definition at line 100 of file complex.cpp.

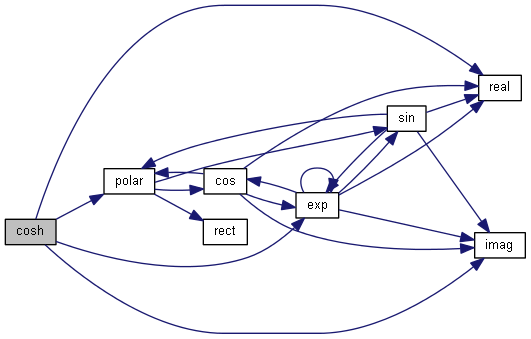
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t cosh ( const nr_complex_t  z)

Compute complex hyperbolic cosinus.

Parameters
[in]zcomplex angle
Returns
hyperbolic cosinus of z

Definition at line 132 of file complex.cpp.

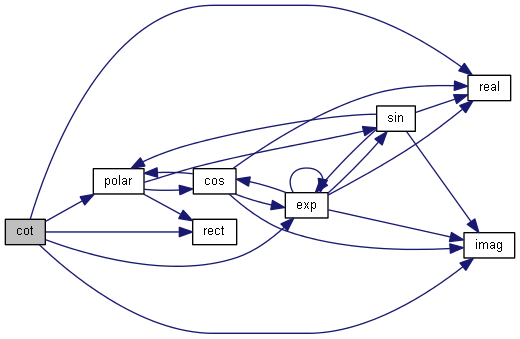
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t cot ( const nr_complex_t  z)

Compute complex cotangent.

Parameters
[in]zcomplex angle
Returns
cotangent of z

Definition at line 403 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t coth ( const nr_complex_t  z)

Compute complex hyperbolic cotangent.

Parameters
[in]zcomplex angle
Returns
hyperbolic cotangent of z

Definition at line 433 of file complex.cpp.

Here is the call graph for this function:

nr_double_t dB ( const nr_complex_t  z)

Magnitude in dB.

Compute $10\log_{10} |z|^2=20\log_{10} |z|$

Parameters
[in]zcomplex number
Returns
Magnitude in dB
Todo:
Why not inline?

Definition at line 455 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t erf ( const nr_complex_t  z)

Error function.

Parameters
[in]zargument
Returns
Error function
Bug:
Not implemented

Definition at line 759 of file complex.cpp.

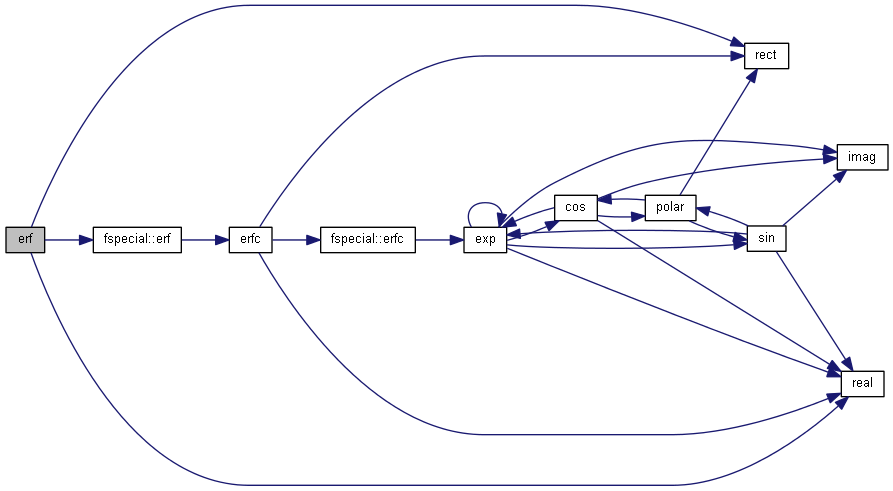
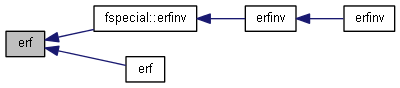
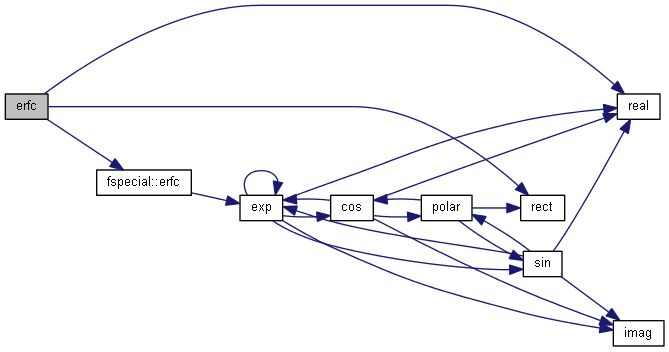
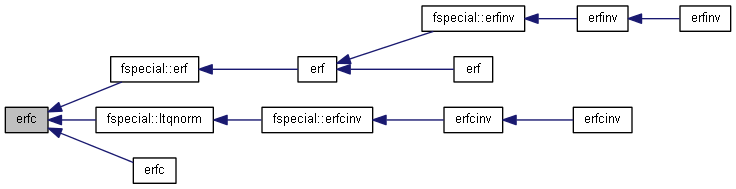
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t erfc ( const nr_complex_t  z)

Complementart error function.

Parameters
[in]zargument
Returns
Complementary error function
Bug:
Not implemented

Definition at line 769 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t erfcinv ( const nr_complex_t  z)

Inverse of complementart error function.

Parameters
[in]zargument
Returns
Inverse of complementary error function
Bug:
Not implemented

Definition at line 789 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t erfinv ( const nr_complex_t  z)

Inverse of error function.

Parameters
[in]zargument
Returns
Inverse of error function
Bug:
Not implemented

Definition at line 779 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t exp ( const nr_complex_t  z)

Compute complex exponential.

Parameters
[in]zcomplex number
Returns
exponential of z

Definition at line 156 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t fix ( const nr_complex_t  z)

Complex ceil.

Apply fix to real and imaginary part

Parameters
[in]zcomplex number
Returns
fixed complex number
Todo:

Why not inline?

why not using real fix

Definition at line 651 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t floor ( const nr_complex_t  z)

Complex floor.

floor is the largest integral value not greater than argument Apply floor to real and imaginary part

Parameters
[in]zcomplex number
Returns
floored complex number
Todo:

Why not inline?

Move near ceil

Definition at line 506 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t fmod ( const nr_complex_t  x,
const nr_complex_t  y 
)

Complex fmod Apply fmod to the complex z.

Parameters
[in]xcomplex number (dividant)
[in]ycomplex number (divisor)
Returns
return $x - n * y$ where n is the quotient of $x / y$, rounded towards zero to an integer.
Todo:
Why not inline?

Definition at line 520 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t fmod ( const nr_complex_t  x,
const nr_double_t  y 
)

Complex fmod (double version) Apply fmod to the complex z.

Parameters
[in]xcomplex number (dividant)
[in]ydouble number (divisor)
Returns
return $x - n * y$ where n is the quotient of $x / y$, rounded towards zero to an integer.
Todo:
Why not inline?

Definition at line 533 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t fmod ( const nr_double_t  x,
const nr_complex_t  y 
)

Complex fmod (double version) Apply fmod to the complex z.

Parameters
[in]xdouble number (dividant)
[in]ycomplex number (divisor)
Returns
return $x - n * y$ where n is the quotient of $x / y$, rounded towards zero to an integer.
Todo:
Why not inline?

Definition at line 546 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t i0 ( const nr_complex_t  z)

Modified Bessel function of first kind.

Parameters
[in]zargument
Returns
Modified Bessel function of first kind of order 0
Bug:
Not implemented

Definition at line 749 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t jn ( const int  n,
const nr_complex_t  z 
)

Bessel function of first kind.

Parameters
[in]norder
[in]zargument
Returns
Bessel function of first kind of order n
Bug:
Not implemented

Definition at line 728 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t limexp ( const nr_complex_t  z)

Compute limited complex exponential.

Parameters
[in]zcomplex number
Returns
limited exponential of z
Todo:
Change limexp(real) limexp(complex) file order

Definition at line 168 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t log ( const nr_complex_t  z)

Compute principal value of natural logarithm of z.

Parameters
[in]zcomplex number
Returns
principal value of natural logarithm of z

Definition at line 179 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t log10 ( const nr_complex_t  z)

Compute principal value of decimal logarithm of z.

Parameters
[in]zcomplex number
Returns
principal value of decimal logarithm of z

Definition at line 191 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t log2 ( const nr_complex_t  z)

Compute principal value of binary logarithm of z.

Parameters
[in]zcomplex number
Returns
principal value of binary logarithm of z

Definition at line 203 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_double_t norm ( const nr_complex_t  z)

Compute euclidian norm of complex number.

Compute $(\Re\mathrm{e}\;z )^2+ (\Im\mathrm{m}\;z)^2=|z|^2$

Parameters
[in]zComplex number
Returns
Euclidian norm of z
Todo:
Why not inline

Definition at line 62 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

bool operator!= ( const nr_complex_t  z1,
const nr_complex_t  z2 
)

Inequality of two complex.

Todo:
Why not inline
Note
Like inequality of double this test is meaningless in finite precision Use instead fabs(x-x0) > tol

Definition at line 809 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t operator% ( const nr_complex_t  z1,
const nr_complex_t  z2 
)

Modulo.

Todo:
Why not inline

Definition at line 844 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t operator% ( const nr_complex_t  z1,
const nr_double_t  r2 
)

Modulo.

Todo:
Why not inline

Definition at line 851 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t operator% ( const nr_double_t  r1,
const nr_complex_t  z2 
)

Modulo.

Todo:
Why not inline

Definition at line 858 of file complex.cpp.

Here is the call graph for this function:

bool operator< ( const nr_complex_t  z1,
const nr_complex_t  z2 
)

Inferior.

Todo:
Why not inline

Definition at line 837 of file complex.cpp.

Here is the call graph for this function:

bool operator<= ( const nr_complex_t  z1,
const nr_complex_t  z2 
)

Inferior of equal.

Todo:
Why not inline

Definition at line 823 of file complex.cpp.

Here is the call graph for this function:

bool operator== ( const nr_complex_t  z1,
const nr_complex_t  z2 
)

Equality of two complex.

Todo:
Why not inline
Note
Like equality of double this test is meaningless in finite precision Use instead fabs(x-x0) < tol

Definition at line 799 of file complex.cpp.

Here is the call graph for this function:

bool operator> ( const nr_complex_t  z1,
const nr_complex_t  z2 
)

Superior.

Todo:
Why not inline

Definition at line 830 of file complex.cpp.

Here is the call graph for this function:

bool operator>= ( const nr_complex_t  z1,
const nr_complex_t  z2 
)

Superior of equal.

Todo:
Why not inline

Definition at line 816 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t polar ( const nr_double_t  mag,
const nr_double_t  ang 
)

Construct a complex number using polar notation.

Parameters
[in]magMagnitude
[in]angAngle
Returns
complex number in rectangular form
Todo:
Why not inline

Definition at line 76 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t polar ( const nr_complex_t  a,
const nr_complex_t  p 
)

Extension of polar construction to complex.

Parameters
[in]aMagnitude
[in]pAngle
Returns
complex number in rectangular form
Bug:
Do not seems holomorph form of real polar
Todo:
Move near real polar

Definition at line 89 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t polar ( const nr_double_t  a,
const nr_complex_t  p 
)
nr_complex_t polar ( const nr_complex_t  a,
const nr_double_t  p = 0.0 
)
nr_complex_t pow ( const nr_complex_t  z,
const nr_double_t  d 
)

Compute power function with real exponent.

Parameters
[in]zcomplex mantisse
[in]dreal exponent
Returns
z power d ( $z^d$)

Definition at line 216 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t pow ( const nr_double_t  d,
const nr_complex_t  z 
)

Compute power function with complex exponent but real mantisse.

Parameters
[in]dreal mantisse
[in]zcomplex exponent
Returns
d power z ( $d^z$)

Definition at line 226 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t pow ( const nr_complex_t  z1,
const nr_complex_t  z2 
)

Compute complex power function.

Parameters
[in]z1complex mantisse
[in]z2complex exponent
Returns
d power z ( $z_1^{z_2}$)

Definition at line 236 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t rect ( const nr_double_t  x,
const nr_double_t  y 
)

Construct a complex number using rectangular notation.

Parameters
[in]xReal part
[in]yImagninary part
Returns
complex number in rectangular form
Todo:

Why not inline?

Move before polar

Definition at line 50 of file complex.cpp.

nr_complex_t round ( const nr_complex_t  z)

Complex round round is the nearest integral value Apply round to real and imaginary part.

Parameters
[in]zcomplex number
Returns
rounded complex number
Todo:
Why not inline?

Definition at line 666 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t rtoy ( const nr_complex_t  r,
nr_complex_t  zref 
)

Converts reflexion coefficient to admittance.

Parameters
[in]rreflexion coefficient
[in]zrefnormalisation impedance
Returns
admittance

Definition at line 492 of file complex.cpp.

Here is the caller graph for this function:

nr_complex_t rtoz ( const nr_complex_t  r,
nr_complex_t  zref 
)

Converts reflexion coefficient to impedance.

Parameters
[in]rreflexion coefficient
[in]zrefnormalisation impedance
Returns
impedance

Definition at line 483 of file complex.cpp.

Here is the caller graph for this function:

nr_complex_t sign ( const nr_complex_t  z)

complex sign function

compute

\[ \mathrm{sign}\;z= \mathrm{sign} (re^{i\theta}) = \begin{cases} 1 & \text{if } z=0 \\ e^{i\theta} & \text{else} \end{cases} \]

Parameters
[in]zcomplex number
Returns
sign of z
Todo:
Better implementation z/abs(z) is not really stable

Definition at line 583 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t signum ( const nr_complex_t  z)

complex signum function

compute

\[ \mathrm{signum}\;z= \mathrm{signum} (re^{i\theta}) = \begin{cases} 0 & \text{if } z=0 \\ e^{i\theta} & \text{else} \end{cases} \]

Parameters
[in]zcomplex number
Returns
signum of z
Todo:
Better implementation z/abs(z) is not really stable

Definition at line 565 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t sin ( const nr_complex_t  z)

Compute complex sinus.

Parameters
[in]zcomplex angle
Returns
sinus of z

Definition at line 247 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t sinc ( const nr_complex_t  z)

Cardinal sinus.

Compute $\mathrm{sinc}\;z=\frac{\sin z}{z}$

Parameters
[in]zcomplex number
Returns
cardianal sinus of z
Todo:
Why not inline

Definition at line 627 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t sinh ( const nr_complex_t  z)

Compute complex hyperbolic sinus.

Parameters
[in]zcomplex angle
Returns
hyperbolic sinus of z

Definition at line 273 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t sqr ( const nr_complex_t  z)

Square of complex number.

Parameters
[in]zcomplex number
Returns
squared complex number
Todo:
Why not inline?

Definition at line 687 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t sqrt ( const nr_complex_t  z)

Compute principal value of square root.

Compute the square root of a given complex number (except negative real), and with a branch cut along the negative real axis.

Parameters
[in]zcomplex number
Returns
principal value of square root z

Definition at line 300 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t step ( const nr_complex_t  z)

Heaviside step function for complex number.

Apply Heaviside to real and imaginary part

Parameters
[in]zHeaviside argument
Returns
Heaviside step
Todo:

Create Heaviside alias

Why not using real heaviside

Definition at line 701 of file complex.cpp.

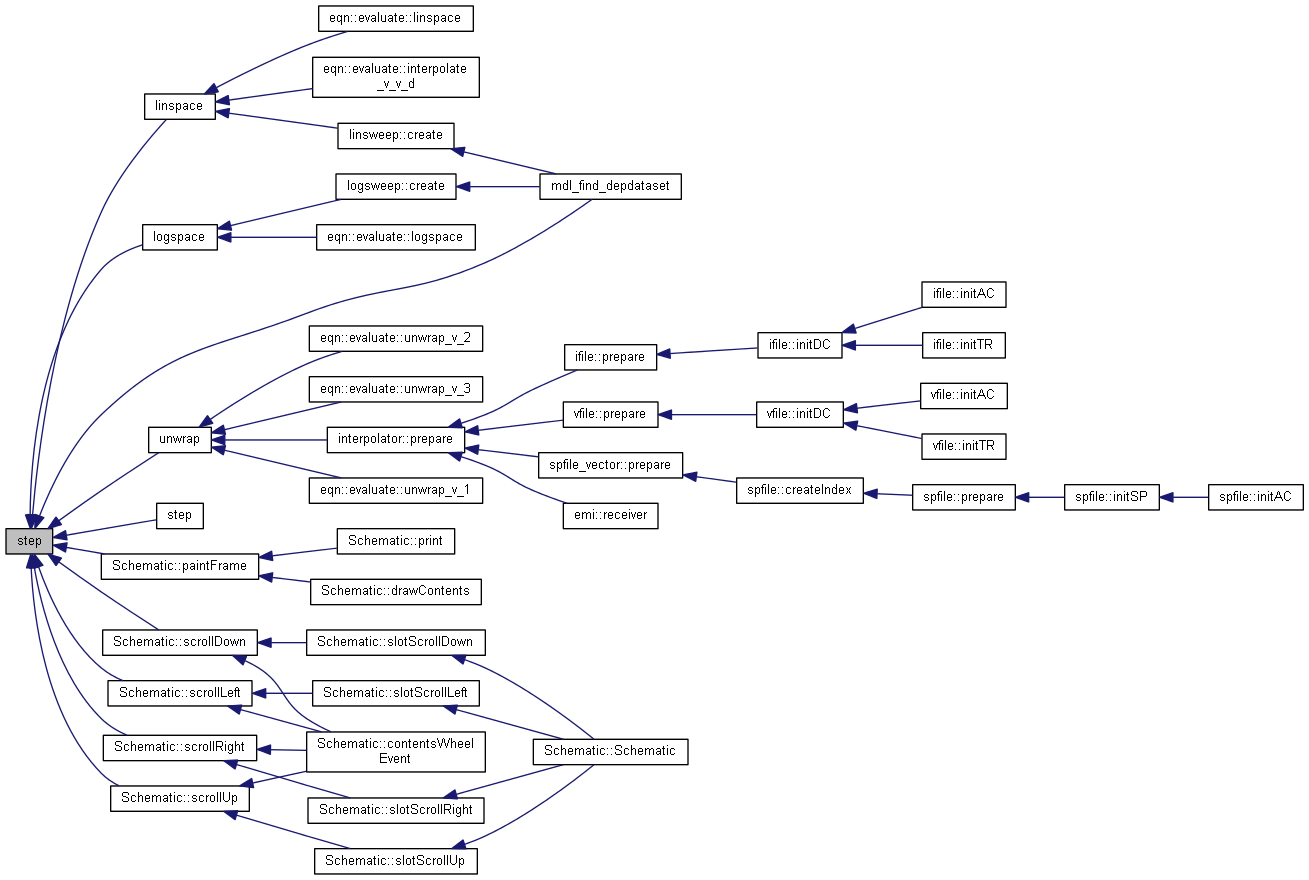
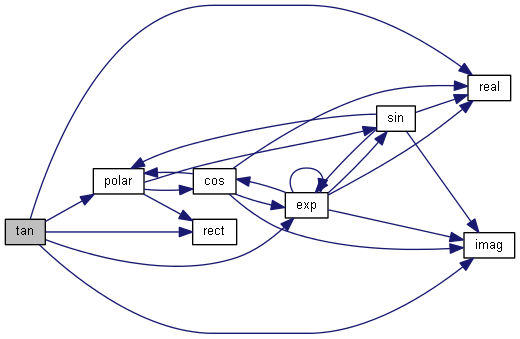
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t tan ( const nr_complex_t  z)

Compute complex tangent.

Parameters
[in]zcomplex angle
Returns
tangent of z

Definition at line 341 of file complex.cpp.

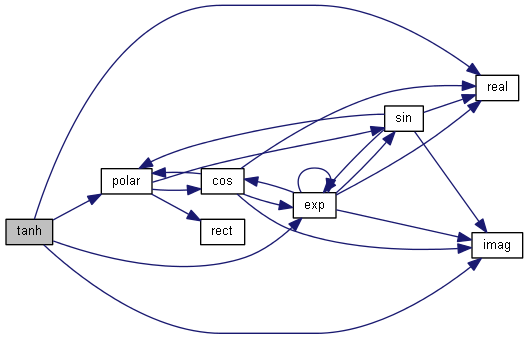
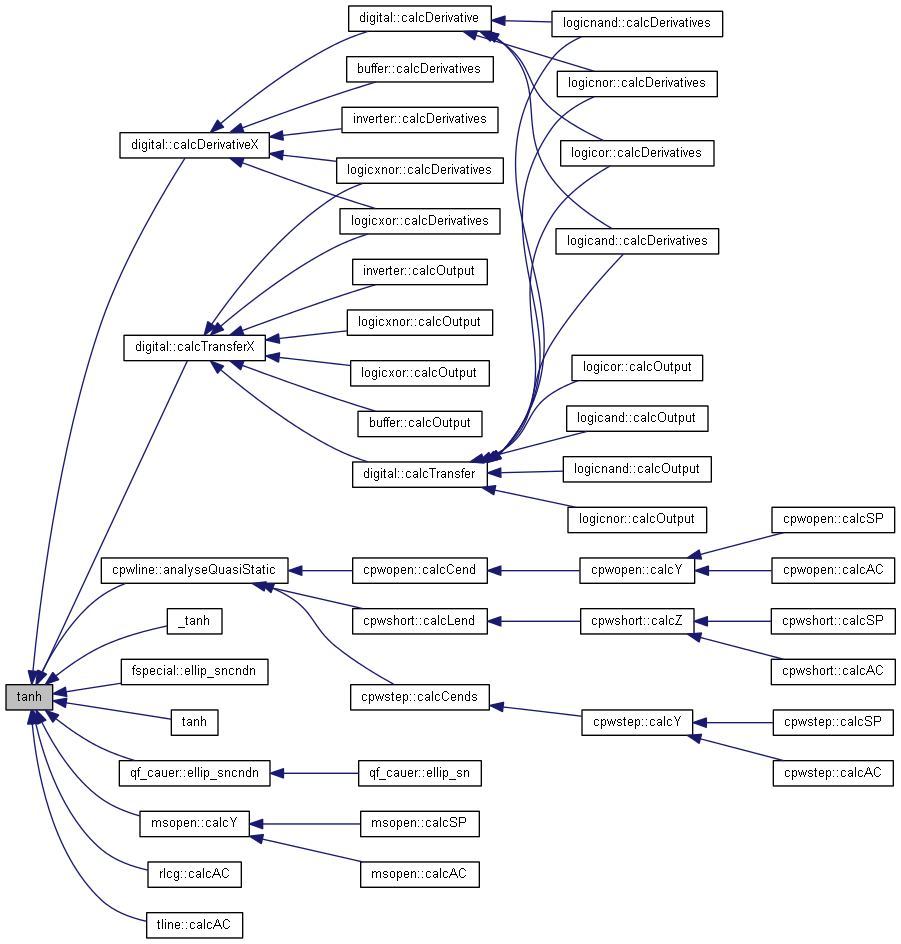
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t tanh ( const nr_complex_t  z)

Compute complex hyperbolic tangent.

Parameters
[in]zcomplex angle
Returns
hyperbolic tangent of z

Definition at line 380 of file complex.cpp.

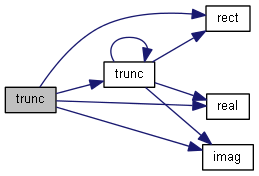
Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t trunc ( const nr_complex_t  z)

Complex trunc.

Apply round to integer, towards zero to real and imaginary part

Parameters
[in]zcomplex number
Returns
rounded complex number
Todo:
Why not inline?

Definition at line 677 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

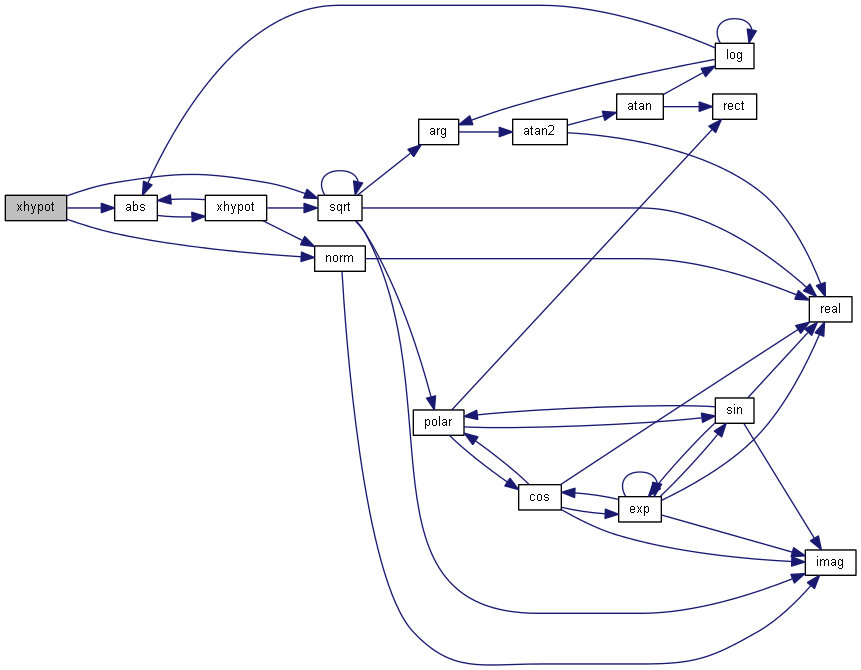
nr_double_t xhypot ( const nr_complex_t  a,
const nr_complex_t  b 
)

Euclidean distance function for complex argument.

The xhypot() function returns $\sqrt{a^2+b^2}$. This is the length of the hypotenuse of a right-angle triangle with sides of length a and b, or the distance of the point (a,b) from the origin.

Parameters
[in]afirst length
[in]bsecond length
Returns
Euclidean distance from (0,0) to (a,b): $\sqrt{a^2+b^2}$

Definition at line 599 of file complex.cpp.

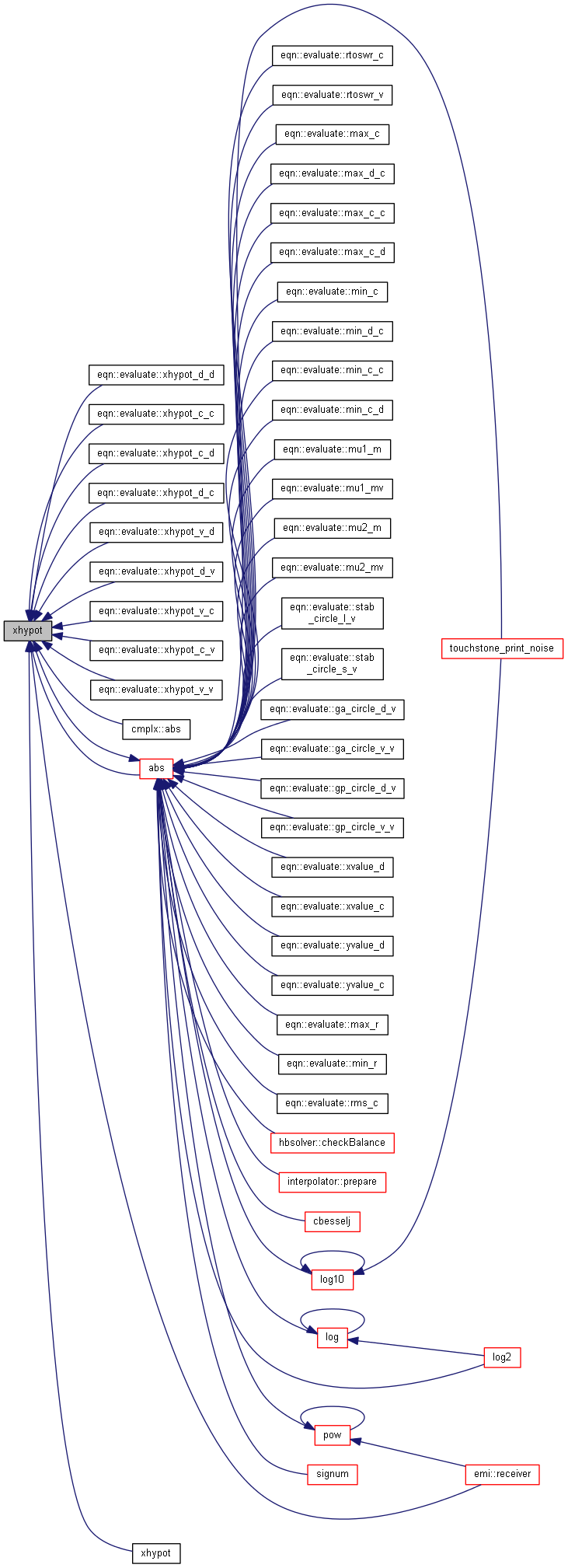
Here is the call graph for this function:

Here is the caller graph for this function:

nr_double_t xhypot ( const nr_double_t  ,
const nr_complex_t   
)

Euclidean distance function for a double b complex.

Definition at line 611 of file complex.cpp.

Here is the call graph for this function:

nr_double_t xhypot ( const nr_complex_t  ,
const nr_double_t   
)

Euclidean distance function for b double a complex.

Definition at line 616 of file complex.cpp.

Here is the call graph for this function:

nr_complex_t yn ( const int  n,
const nr_complex_t  z 
)

Bessel function of second kind.

Parameters
[in]norder
[in]zargument
Returns
Bessel function of second kind of order n
Bug:
Not implemented

Definition at line 739 of file complex.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

nr_complex_t ytor ( const nr_complex_t  y,
nr_complex_t  zref 
)

Converts admittance to reflexion coefficient.

Parameters
[in]yadmitance
[in]zrefnormalisation impedance
Returns
reflexion coefficient

Definition at line 474 of file complex.cpp.

Here is the caller graph for this function:

nr_complex_t ztor ( const nr_complex_t  z,
nr_complex_t  zref 
)

Converts impedance to reflexion coefficient.

Parameters
[in]zimpedance
[in]zrefnormalisation impedance
Returns
reflexion coefficient

Definition at line 465 of file complex.cpp.

Here is the caller graph for this function:

Generated on Tue Dec 25 2012 14:31:12 for My Project by   doxygen 1.8.2