My Project  0.0.16
QUCS Mapping
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Pages
Public Member Functions | Friends | List of all members
matrix Class Reference

Dense complex matrix class. More...

#include <matrix.h>

Public Member Functions

 matrix ()
 Create an empty matrix.
 
 matrix (int)
 Creates a square matrix.
 
 matrix (int, int)
 
 matrix (const matrix &)
 
const matrix & operator= (const matrix &)
 Assignment operator.
 
 ~matrix ()
 
nr_complex_t get (int, int)
 Returns the matrix element at the given row and column.
 
void set (int, int, nr_complex_t)
 Sets the matrix element at the given row and column.
 
int getCols (void)
 
int getRows (void)
 
nr_complex_t * getData (void)
 
void print (void)
 
void exchangeRows (int, int)
 The function swaps the given rows with each other.
 
void exchangeCols (int, int)
 The function swaps the given column with each other.
 
matrix operator- ()
 Unary minus.
 
matrix operator+= (matrix)
 Intrinsic matrix addition.
 
matrix operator-= (matrix)
 Intrinsic matrix subtraction.
 
nr_complex_t operator() (int r, int c) const
 Read access operator.
 
nr_complex_t & operator() (int r, int c)
 Write access operator.
 

Friends

matrix operator+ (matrix, matrix)
 Matrix addition.
 
matrix operator+ (nr_complex_t, matrix)
 Complex scalar addition different order.
 
matrix operator+ (matrix, nr_complex_t)
 Complex scalar addition.
 
matrix operator+ (nr_double_t, matrix)
 Real scalar addition different order.
 
matrix operator+ (matrix, nr_double_t)
 Real scalar addition.
 
matrix operator- (matrix, matrix)
 Matrix subtraction.
 
matrix operator- (nr_complex_t, matrix)
 Complex scalar substraction different order.
 
matrix operator- (matrix, nr_complex_t)
 Complex scalar substraction.
 
matrix operator- (nr_double_t, matrix)
 Real scalar substraction different order.
 
matrix operator- (matrix, nr_double_t)
 Real scalar substraction.
 
matrix operator/ (matrix, nr_complex_t)
 Matrix scaling division by complex version.
 
matrix operator/ (matrix, nr_double_t)
 Matrix scaling division by real version.
 
matrix operator* (nr_complex_t, matrix)
 Matrix scaling complex version (different order)
 
matrix operator* (matrix, nr_complex_t)
 Matrix scaling complex version.
 
matrix operator* (nr_double_t, matrix)
 Matrix scaling real version (different order)
 
matrix operator* (matrix, nr_double_t)
 Matrix scaling complex version.
 
matrix operator* (matrix, matrix)
 
matrix transpose (matrix)
 Matrix transposition.
 
matrix conj (matrix)
 Conjugate complex matrix.
 
matrix abs (matrix)
 Computes magnitude of each matrix element.
 
matrix dB (matrix)
 Computes magnitude in dB of each matrix element.
 
matrix arg (matrix)
 Computes the argument of each matrix element.
 
matrix adjoint (matrix)
 adjoint matrix
 
matrix real (matrix)
 Real part matrix.
 
matrix imag (matrix)
 Imaginary part matrix.
 
matrix eye (int, int)
 Create identity matrix with specified number of rows and columns.
 
matrix diagonal (vector)
 Create a diagonal matrix from a vector.
 
matrix pow (matrix, int)
 
nr_complex_t cofactor (matrix, int, int)
 Computes the complex cofactor of the given determinant.
 
nr_complex_t detLaplace (matrix)
 Compute determinant of the given matrix using Laplace expansion.
 
nr_complex_t detGauss (matrix)
 Compute determinant Gaussian algorithm.
 
nr_complex_t det (matrix)
 Compute determinant of the given matrix.
 
matrix inverseLaplace (matrix)
 Compute inverse matrix using Laplace expansion.
 
matrix inverseGaussJordan (matrix)
 Compute inverse matrix using Gauss-Jordan elimination.
 
matrix inverse (matrix)
 Compute inverse matrix.
 
matrix stos (matrix, nr_complex_t, nr_complex_t z0=50.0)
 S renormalization with all part identic.
 
matrix stos (matrix, nr_double_t, nr_double_t z0=50.0)
 S renormalization with all part identic and real.
 
matrix stos (matrix, vector, nr_complex_t z0=50.0)
 S renormalization (variation)
 
matrix stos (matrix, nr_complex_t, vector)
 S renormalization (variation)
 
matrix stos (matrix, vector, vector)
 S params to S params.
 
matrix stoz (matrix, nr_complex_t z0=50.0)
 Scattering parameters to impedance matrix identic case.
 
matrix stoz (matrix, vector)
 Scattering parameters to impedance matrix.
 
matrix ztos (matrix, nr_complex_t z0=50.0)
 Convert impedance matrix to scattering parameters identic case.
 
matrix ztos (matrix, vector)
 Convert impedance matrix scattering parameters.
 
matrix ztoy (matrix)
 impedance matrix to admittance matrix.
 
matrix stoy (matrix, nr_complex_t z0=50.0)
 Convert scattering pto adminttance parameters identic case.
 
matrix stoy (matrix, vector)
 Scattering parameters to admittance matrix.
 
matrix ytos (matrix, nr_complex_t z0=50.0)
 Convert Admittance matrix to scattering parameters identic case.
 
matrix ytos (matrix, vector)
 Admittance matrix to scattering parameters.
 
matrix ytoz (matrix)
 Convert admittance matrix to impedance matrix.
 
matrix stoa (matrix, nr_complex_t z1=50.0, nr_complex_t z2=50.0)
 Converts chain matrix to scattering parameters.
 
matrix atos (matrix, nr_complex_t z1=50.0, nr_complex_t z2=50.0)
 Converts chain matrix to scattering parameters.
 
matrix stoh (matrix, nr_complex_t z1=50.0, nr_complex_t z2=50.0)
 Converts scattering parameters to hybrid matrix.
 
matrix htos (matrix, nr_complex_t z1=50.0, nr_complex_t z2=50.0)
 Converts hybrid matrix to scattering parameters.
 
matrix stog (matrix, nr_complex_t z1=50.0, nr_complex_t z2=50.0)
 
matrix gtos (matrix, nr_complex_t z1=50.0, nr_complex_t z2=50.0)
 
matrix cytocs (matrix, matrix)
 Admittance noise correlation matrix to S-parameter noise correlation matrix.
 
matrix cztocs (matrix, matrix)
 Converts impedance noise correlation matrix to S-parameter noise correlation matrix.
 
matrix cztocy (matrix, matrix)
 Converts impedance noise correlation matrix to admittance noise correlation matrix.
 
matrix cstocy (matrix, matrix)
 Converts S-parameter noise correlation matrix to admittance noise correlation matrix.
 
matrix cytocz (matrix, matrix)
 Converts admittance noise correlation matrix to impedance noise correlation matrix.
 
matrix cstocz (matrix, matrix)
 Converts S-parameter noise correlation matrix to impedance noise correlation matrix.
 
matrix twoport (matrix, char, char)
 Generic conversion matrix.
 
nr_double_t rollet (matrix)
 
nr_double_t b1 (matrix)
 

Detailed Description

Dense complex matrix class.

Definition at line 34 of file matrix.h.

Constructor & Destructor Documentation

matrix::matrix ( )

Create an empty matrix.

Constructor creates an unnamed instance of the matrix class.

Definition at line 102 of file matrix.cpp.

matrix::matrix ( int  s)

Creates a square matrix.

Constructor creates an unnamed instance of the matrix class with a certain number of rows and columns. Particularly creates a square matrix.

Parameters
[in]snumber of rows or colums of square matrix
Todo:
Why not s const?

Definition at line 115 of file matrix.cpp.

matrix::matrix ( int  r,
int  c 
)

Definition at line 129 of file matrix.cpp.

matrix::matrix ( const matrix &  m)

Definition at line 141 of file matrix.cpp.

matrix::~matrix ( )

Destructor

Destructor deletes a matrix object.

Definition at line 182 of file matrix.cpp.

Member Function Documentation

void matrix::exchangeCols ( int  c1,
int  c2 
)

The function swaps the given column with each other.

Parameters
[in]c1source column
[in]c2destination column
Note
assert not out of bound r1 and r2
Todo:
c1 and c2 const

Definition at line 1552 of file matrix.cpp.

void matrix::exchangeRows ( int  r1,
int  r2 
)

The function swaps the given rows with each other.

Parameters
[in]r1source row
[in]r2destination row
Note
assert not out of bound r1 and r2
Todo:
r1 and r2 const

Definition at line 1534 of file matrix.cpp.

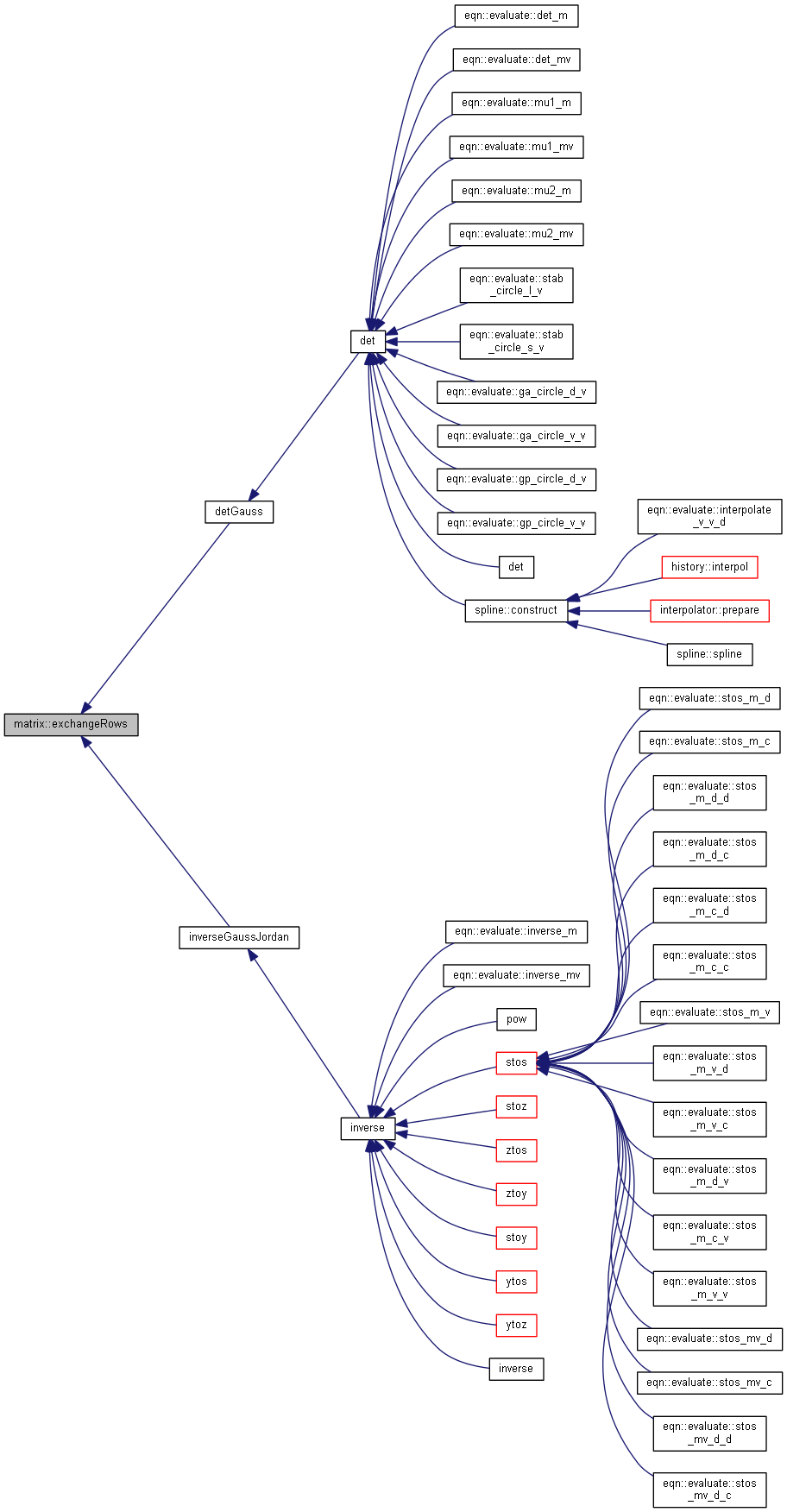
Here is the caller graph for this function:

nr_complex_t matrix::get ( int  r,
int  c 
)

Returns the matrix element at the given row and column.

Parameters
[in]rrow number
[in]ccolumn number
Todo:

Why not inline and synonymous of ()

c and r const

Definition at line 192 of file matrix.cpp.

Here is the caller graph for this function:

int matrix::getCols ( void  )
inline

Definition at line 45 of file matrix.h.

nr_complex_t* matrix::getData ( void  )
inline

Definition at line 47 of file matrix.h.

Here is the caller graph for this function:

int matrix::getRows ( void  )
inline

Definition at line 46 of file matrix.h.

nr_complex_t matrix::operator() ( int  r,
int  c 
) const
inline

Read access operator.

Parameters
[in]r,:row number (from 0 like usually in C)
[in]c,:column number (from 0 like usually in C)
Returns
Cell in the row r and column c
Todo:

: Why not inline

: Why not r and c not const

: Create a debug version checking out of bound (using directly assert)

Definition at line 135 of file matrix.h.

nr_complex_t& matrix::operator() ( int  r,
int  c 
)
inline

Write access operator.

Parameters
[in]r,:row number (from 0 like usually in C)
[in]c,:column number (from 0 like usually in C)
Returns
Reference to cell in the row r and column c
Todo:

: Why not inline

: Why r and c not const

: Create a debug version checking out of bound (using directly assert)

Definition at line 144 of file matrix.h.

matrix matrix::operator+= ( matrix  a)

Intrinsic matrix addition.

Parameters
[in]amatrix to add
Note
assert same size
Todo:
a is const

Definition at line 241 of file matrix.cpp.

Here is the call graph for this function:

matrix matrix::operator- ( )

Unary minus.

Definition at line 268 of file matrix.cpp.

Here is the call graph for this function:

matrix matrix::operator-= ( matrix  a)

Intrinsic matrix subtraction.

Parameters
[in]amatrix to substract
Note
assert same size

Definition at line 281 of file matrix.cpp.

Here is the call graph for this function:

const matrix & matrix::operator= ( const matrix &  m)

Assignment operator.

The assignment copy constructor creates a new instance based on the given matrix object.

Parameters
[in]mobject to copy
Returns
assigned object
Note
m = m is safe

Definition at line 162 of file matrix.cpp.

void matrix::print ( void  )
void matrix::set ( int  r,
int  c,
nr_complex_t  z 
)

Sets the matrix element at the given row and column.

Parameters
[in]rrow number
[in]ccolumn number
[in]zcomplex number to assign
Todo:

Why not inline and synonymous of ()

r c and z const

Definition at line 203 of file matrix.cpp.

Here is the caller graph for this function:

Friends And Related Function Documentation

matrix abs ( matrix  a)
friend

Computes magnitude of each matrix element.

Parameters
[in]amatrix
Todo:

add abs in place

a is const

Definition at line 529 of file matrix.cpp.

matrix adjoint ( matrix  a)
friend

adjoint matrix

The function returns the adjoint complex matrix. This is also called the adjugate or transpose conjugate.

Parameters
[in]aMatrix to transpose
Todo:

add adjoint in place

Do not lazy and avoid conj and transpose copy

a is const

Definition at line 520 of file matrix.cpp.

matrix arg ( matrix  a)
friend

Computes the argument of each matrix element.

Parameters
[in]amatrix
Todo:

add arg in place

a is const

Definition at line 553 of file matrix.cpp.

matrix atos ( matrix  a,
nr_complex_t  z1 = 50.0,
nr_complex_t  z2 = 50.0 
)
friend

Converts chain matrix to scattering parameters.

Converts chain matrix to scattering parameters Formulae are given by [5] and are remembered here:

\begin{align*} S_{11}&=\frac{AZ_{02}+B-CZ_{01}^*Z_{02}-DZ_{01}^*}{\Delta} \\ S_{12}&=\frac{2(AD-BC) (\Re\text{e}\;Z_{01}\Re\text{e}\;Z_{02})^{1/2}} {\Delta}\\ S_{21}&=\frac{2(\Re\text{e}\;Z_{01}\Re\text{e}\;Z_{02})^{1/2}}{\Delta}\\ S_{22}&=\frac{-AZ_{02}^*+B-CZ_{01}^*Z_{02}+DZ_{01}}{\Delta} \end{align*}

Where:

\[ \Delta =AZ_{02}+B+CZ_{01}Z_{02}-DZ_{01} \]

Parameters
[in]aChain matrix
[in]z1impedance at input 1
[in]z2impedance at input 2
Returns
Scattering matrix
Bug:
Do not use fabs
Todo:
a, z1, z2 const

Definition at line 1213 of file matrix.cpp.

nr_double_t b1 ( matrix  )
friend
nr_complex_t cofactor ( matrix  a,
int  u,
int  v 
)
friend

Computes the complex cofactor of the given determinant.

The cofactor is the determinant obtained by deleting the row and column of a given element of a matrix or determinant. The cofactor is preceded by a + or - sign depending of the sign of $(-1)^(u+v)$

Bug:
This algortihm is recursive! Stack overfull!
Todo:

((u + v) & 1) is cryptic use (u + v)% 2

#ifdef 0

static?

Definition at line 648 of file matrix.cpp.

matrix conj ( matrix  a)
friend

Conjugate complex matrix.

Parameters
[in]aMatrix to conjugate
Todo:

add conj in place

a is const

Definition at line 503 of file matrix.cpp.

matrix cstocy ( matrix  cs,
matrix  y 
)
friend

Converts S-parameter noise correlation matrix to admittance noise correlation matrix.

According to [7] fig 2:

\[ C_y=(I+Y)C_s(I+Y)^+ \]

Where $C_s$ is the scattering noise correlation matrix, $C_y$ the admittance noise correlation matrix, $I$ the identity matrix and $S$ the scattering matrix of device. $x^+$ is the adjoint of $x$

Warning
cs matrix and y matrix are assumed to be normalized
Parameters
[in]csS parameter noise correlation
[in]yAdmittance matrix of device
Returns
admittance noise correlation matrix
Todo:
cs, y const

Definition at line 1421 of file matrix.cpp.

matrix cstocz ( matrix  cs,
matrix  z 
)
friend

Converts S-parameter noise correlation matrix to impedance noise correlation matrix.

According to [7] fig 2:

\[ C_z=(I+Z)C_s(I+Z)^+ \]

Where $C_s$ is the scattering noise correlation matrix, $C_z$ the impedance noise correlation matrix, $I$ the identity matrix and $S$ the scattering matrix of device. $x^+$ is the adjoint of $x$

Warning
cs matrix and y matrix are assumed to be normalized
Parameters
[in]csS parameter noise correlation
[in]zImpedance matrix of device
Returns
Impedance noise correlation matrix
Todo:
cs, z const

Definition at line 1474 of file matrix.cpp.

matrix cytocs ( matrix  cy,
matrix  s 
)
friend

Admittance noise correlation matrix to S-parameter noise correlation matrix.

Converts admittance noise correlation matrix to S-parameter noise correlation matrix. According to [7] fig 2:

\[ C_s=\frac{1}{4}(I+S)C_y(I+S)^+ \]

Where $C_s$ is the scattering noise correlation matrix, $C_y$ the admittance noise correlation matrix, $I$ the identity matrix and $S$ the scattering matrix of device. $x^+$ is the adjoint of $x$

Warning
cy matrix and s matrix are assumed to be normalized
Parameters
[in]cyAdmittance noise correlation
[in]sS parameter matrix of device
Returns
S-parameter noise correlation matrix
Note
Assert compatiblity of matrix
Todo:
cy s const

Definition at line 1395 of file matrix.cpp.

matrix cytocz ( matrix  cy,
matrix  z 
)
friend

Converts admittance noise correlation matrix to impedance noise correlation matrix.

According to [7] fig 2:

\[ C_z=ZC_yZ^+ \]

Where $C_z$ is the impedance correlation matrix, $I$ the identity matrix and $C_y$ the admittance noise correlation matrix. $x^+$ is the adjoint of $x$

Warning
cy matrix and z matrix are assumed to be normalized
Parameters
[in]cyAdmittance noise correlation
[in]zImpedance matrix of device
Returns
Impedance noise correlation matrix
Todo:
cs, z const

Definition at line 1522 of file matrix.cpp.

matrix cztocs ( matrix  cz,
matrix  s 
)
friend

Converts impedance noise correlation matrix to S-parameter noise correlation matrix.

According to [7] fig 2:

\[ C_s=\frac{1}{4}(I-S)C_z(I-S) \]

Where $C_s$ is the scattering noise correlation matrix, $C_z$ the impedance noise correlation matrix, $I$ the identity matrix and $S$ the scattering matrix of device. $x^+$ is the adjoint of $x$

Warning
Cz matrix and s matrix are assumed to be normalized
Parameters
[in]czImpedance noise correlation
[in]sS parameter matrix of device
Returns
S-parameter noise correlation matrix
Note
Assert compatiblity of matrix
Todo:
cz, s const

Definition at line 1448 of file matrix.cpp.

matrix cztocy ( matrix  cz,
matrix  y 
)
friend

Converts impedance noise correlation matrix to admittance noise correlation matrix.

According to [7] fig 2:

\[ C_y=YC_zY^+ \]

Where $C_z$ is the impedance correlation matrix, $I$ the identity matrix and $C_y$ the admittance noise correlation matrix. $x^+$ is the adjoint of $x$

Warning
cz matrix and y matrix are assumed to be normalized
Parameters
[in]czimpedance noise correlation
[in]yAdmittance matrix of device
Returns
admittance noise correlation matrix
Todo:
cs, y const

Definition at line 1498 of file matrix.cpp.

matrix dB ( matrix  a)
friend

Computes magnitude in dB of each matrix element.

Parameters
[in]amatrix

Definition at line 540 of file matrix.cpp.

nr_complex_t det ( matrix  a)
friend

Compute determinant of the given matrix.

Parameters
[in]amatrix
Returns
Complex determinant
Todo:
a const?

Definition at line 753 of file matrix.cpp.

nr_complex_t detGauss ( matrix  a)
friend

Compute determinant Gaussian algorithm.

Compute determinant of the given matrix using the Gaussian algorithm. This means to triangulate the matrix and multiply all the diagonal elements.

Parameters
[in]amatrix
Note
assert square matrix
Todo:

static ?

a const?

Definition at line 708 of file matrix.cpp.

nr_complex_t detLaplace ( matrix  a)
friend

Compute determinant of the given matrix using Laplace expansion.

The Laplace expansion of the determinant of an n by n square matrix a expresses the determinant of a as a sum of n determinants of (n-1) by (n-1) sub-matrices of a. There are 2n such expressions, one for each row and column of a.

See Wikipedia http://en.wikipedia.org/wiki/Laplace_expansion

Parameters
[in]amatrix
Bug:
This algortihm is recursive! Stack overfull!
Note
assert square matrix
Todo:

#ifdef 0

static ?

Definition at line 677 of file matrix.cpp.

matrix diagonal ( vector  diag)
friend

Create a diagonal matrix from a vector.

Parameters
[in]diagvector to write on the diagonal
Todo:
diag is const

Definition at line 615 of file matrix.cpp.

matrix eye ( int  rs,
int  cs 
)
friend

Create identity matrix with specified number of rows and columns.

Parameters
[in]rsrow number
[in]cscolumn number
Todo:

Avoid res.get*

Use memset

rs, cs are const

Definition at line 594 of file matrix.cpp.

matrix gtos ( matrix  g,
nr_complex_t  z1 = 50.0,
nr_complex_t  z2 = 50.0 
)
friend

Definition at line 1346 of file matrix.cpp.

matrix htos ( matrix  h,
nr_complex_t  z1 = 50.0,
nr_complex_t  z2 = 50.0 
)
friend

Converts hybrid matrix to scattering parameters.

Formulae are given by [5] and are remembered here:

\begin{align*} S_{11}&=\frac{(h_{11}-Z_{01}^*)(1+h_{22}Z_{02})-h_{12}h_{21}Z_{02}} {\Delta}\\ S_{12}&=\frac{-2h_{12}(\Re\text{e}\;Z_{01}\Re\text{e}\;Z_{02})^\frac{1}{2}} {\Delta}\\ S_{21}&=\frac{-2h_{21}(\Re\text{e}\;Z_{01}\Re\text{e}\;Z_{02})^\frac{1}{2}} {\Delta}\\ S_{22}&=\frac{(h_{11}+Z_{01})(1-h_{22}Z_{02}^*)-h_{12}h_{21}Z_{02}^*} {\Delta} \end{align*}

Where $\Delta$ is:

\[ \Delta=(Z_{01}+h_{11})(1+h_{22}Z_{02})-h_{12}h_{21}Z_{02} \]

Parameters
[in]hhybrid matrix
[in]z1impedance at input 1
[in]z2impedance at input 2
Returns
scattering matrix
Note
Assert 2 by 2 matrix
Todo:
Why not h,z1,z2 const

Definition at line 1298 of file matrix.cpp.

matrix imag ( matrix  a)
friend

Imaginary part matrix.

Parameters
[in]amatrix
Todo:

add imag in place

a is const

Definition at line 579 of file matrix.cpp.

matrix inverse ( matrix  a)
friend

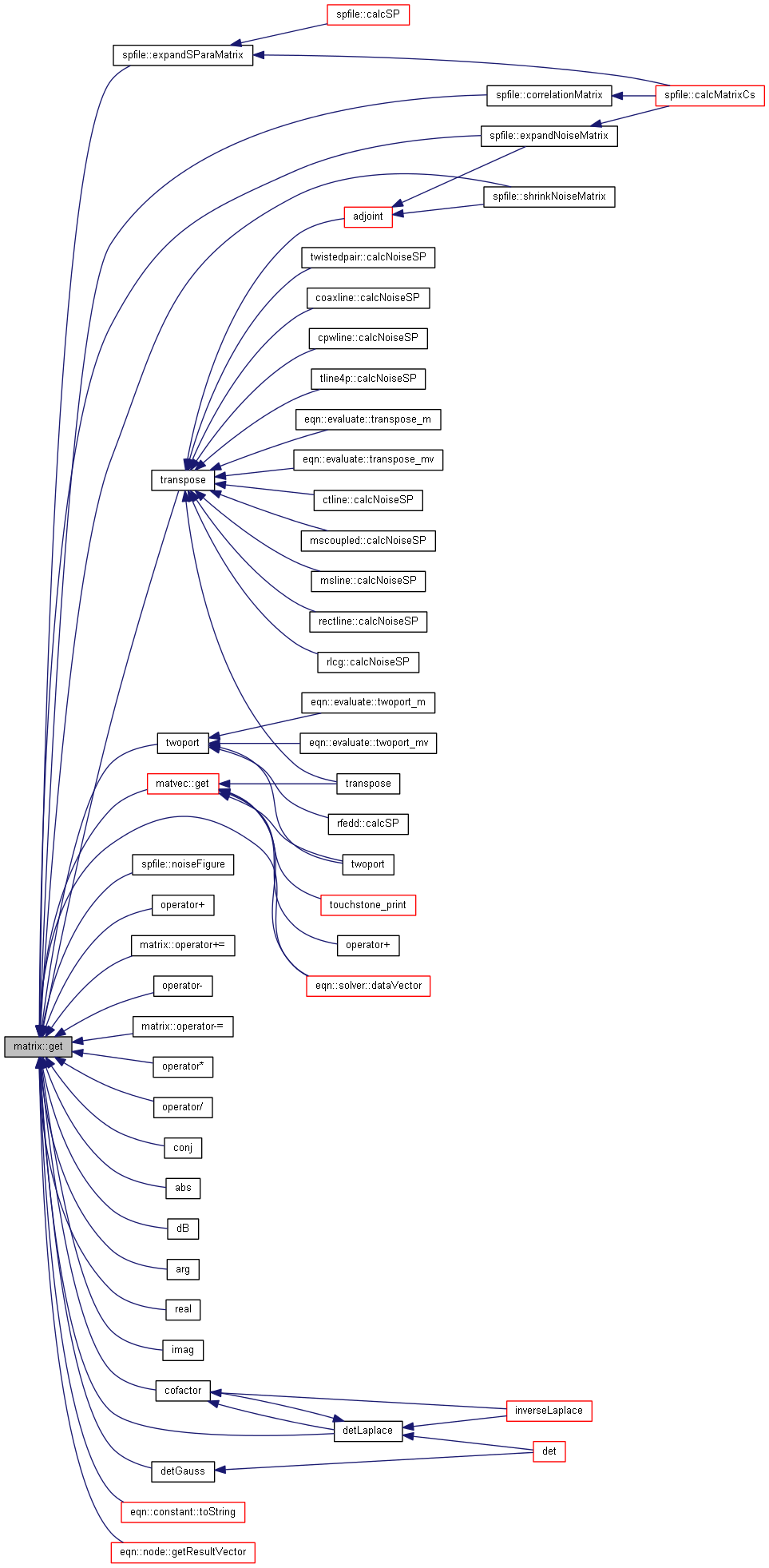
Compute inverse matrix.

Parameters
[in]amatrix to invert
Todo:
a is const

Definition at line 838 of file matrix.cpp.

matrix inverseGaussJordan ( matrix  a)
friend

Compute inverse matrix using Gauss-Jordan elimination.

Compute inverse matrix of the given matrix by Gauss-Jordan elimination.

Todo:

a const?

static?

Note
assert non singulat matix
Parameters
[in]amatrix to invert

Definition at line 789 of file matrix.cpp.

matrix inverseLaplace ( matrix  a)
friend

Compute inverse matrix using Laplace expansion.

Compute inverse matrix of the given matrix using Laplace expansion.

Parameters
[in]amatrix to invert
Todo:

Static?

#ifdef 0

Bug:
recursive! Stack overflow
Todo:
a const?

Definition at line 770 of file matrix.cpp.

matrix operator* ( nr_complex_t  z,
matrix  a 
)
friend

Matrix scaling complex version (different order)

Parameters
[in]amatrix to scale
[in]zscaling complex
Returns
Scaled matrix
Todo:

Why not a and z const

Why not inline

Definition at line 311 of file matrix.cpp.

matrix operator* ( matrix  a,
nr_complex_t  z 
)
friend

Matrix scaling complex version.

Parameters
[in]amatrix to scale
[in]zscaling complex
Returns
Scaled matrix
Todo:
Why not a and z const

Definition at line 296 of file matrix.cpp.

matrix operator* ( nr_double_t  d,
matrix  a 
)
friend

Matrix scaling real version (different order)

Parameters
[in]amatrix to scale
[in]dscaling real
Returns
Scaled matrix
Todo:

Why not inline?

Why not d and a const

Definition at line 336 of file matrix.cpp.

matrix operator* ( matrix  a,
nr_double_t  d 
)
friend

Matrix scaling complex version.

Parameters
[in]amatrix to scale
[in]dscaling real
Returns
Scaled matrix
Todo:
Why not d and a const

Definition at line 321 of file matrix.cpp.

matrix operator* ( matrix  a,
matrix  b 
)
friend

Matrix multiplication.

Dumb and not optimized matrix multiplication

Parameters
a]first matrix
b]second matrix
Note
assert compatibility
Todo:
a and b are const

Definition at line 376 of file matrix.cpp.

matrix operator+ ( matrix  a,
matrix  b 
)
friend

Matrix addition.

Parameters
a]first matrix
b]second matrix
Note
assert same size
Todo:
a and b are const

Definition at line 226 of file matrix.cpp.

matrix operator+ ( nr_complex_t  z,
matrix  a 
)
friend

Complex scalar addition different order.

Parameters
[in]amatrix
[in]zcomplex to add
Todo:

Move near other +

a and z are const

Why not inline

Definition at line 412 of file matrix.cpp.

matrix operator+ ( matrix  a,
nr_complex_t  z 
)
friend

Complex scalar addition.

Parameters
[in]amatrix
[in]zcomplex to add
Todo:

Move near other +

a and z are const

Definition at line 397 of file matrix.cpp.

matrix operator+ ( nr_double_t  d,
matrix  a 
)
friend

Real scalar addition different order.

Parameters
[in]amatrix
[in]dreal to add
Todo:

Move near other +

a and d are const

Why not inline

Definition at line 437 of file matrix.cpp.

matrix operator+ ( matrix  a,
nr_double_t  d 
)
friend

Real scalar addition.

Parameters
[in]amatrix
[in]dreal to add
Todo:

Move near other +

a and d are const

Definition at line 422 of file matrix.cpp.

matrix operator- ( matrix  a,
matrix  b 
)
friend

Matrix subtraction.

Parameters
a]first matrix
b]second matrix
Note
assert same size
Todo:
a and b are const

Definition at line 257 of file matrix.cpp.

matrix operator- ( nr_complex_t  z,
matrix  a 
)
friend

Complex scalar substraction different order.

Parameters
[in]amatrix
[in]zcomplex to add
Todo:

Move near other +

a and z are const

Why not inline

Definition at line 459 of file matrix.cpp.

matrix operator- ( matrix  a,
nr_complex_t  z 
)
friend

Complex scalar substraction.

Parameters
[in]amatrix
[in]zcomplex to add
Todo:

Move near other +

a and z are const

Why not inline

Definition at line 448 of file matrix.cpp.

matrix operator- ( nr_double_t  d,
matrix  a 
)
friend

Real scalar substraction different order.

Parameters
[in]amatrix
[in]zreal to add
Todo:

Move near other +

a and z are const

Why not inline

Definition at line 481 of file matrix.cpp.

matrix operator- ( matrix  a,
nr_double_t  d 
)
friend

Real scalar substraction.

Parameters
[in]amatrix
[in]zreal to add
Todo:

Move near other +

a and z are const

Why not inline

Definition at line 470 of file matrix.cpp.

matrix operator/ ( matrix  a,
nr_complex_t  z 
)
friend

Matrix scaling division by complex version.

Parameters
[in]amatrix to scale
[in]zscaling complex
Returns
Scaled matrix
Todo:
Why not a and z const

Definition at line 346 of file matrix.cpp.

matrix operator/ ( matrix  a,
nr_double_t  d 
)
friend

Matrix scaling division by real version.

Parameters
[in]amatrix to scale
[in]dscaling real
Returns
Scaled matrix
Todo:
Why not a and d const

Definition at line 360 of file matrix.cpp.

matrix pow ( matrix  a,
int  n 
)
friend

Definition at line 623 of file matrix.cpp.

matrix real ( matrix  a)
friend

Real part matrix.

Parameters
[in]amatrix
Todo:

add real in place

a is const

Definition at line 566 of file matrix.cpp.

nr_double_t rollet ( matrix  )
friend
matrix stoa ( matrix  s,
nr_complex_t  z1 = 50.0,
nr_complex_t  z2 = 50.0 
)
friend

Converts chain matrix to scattering parameters.

Converts scattering parameters to chain matrix. Formulae are given by [5] tab 1. and are remembered here:

\begin{align*} A&=\frac{(Z_{01}^*+S_{11}Z_{01})(1-S_{22}) +S_{12}S_{21}Z_{01}}{\Delta} \\ B&=\frac{(Z_{01}^*+S_{11}Z_{01})(Z_{02}^*+S_{22}Z_{02}) -S_{12}S_{21}Z_{01}Z_{02}}{\Delta} \\ C&=\frac{(1-S_{11})(1-S_{22}) -S_{12}S_{21}}{\Delta} \\ D&=\frac{(1-S_{11})(Z_{02}^*+S_{22}Z_{02}) +S_{12}S_{21}Z_{02}}{\Delta} \end{align*}

Where:

\[ \Delta = 2 S_{21}\sqrt{\Re\text{e}\;Z_{01}\Re\text{e}\;Z_{02}} \]

Bug:
Do not need fabs
Parameters
[in]sScattering matrix
[in]z1impedance at input 1
[in]z2impedance at input 2
Returns
Chain matrix
Note
Assert 2 by 2 matrix
Todo:
Why not s,z1,z2 const

Definition at line 1172 of file matrix.cpp.

matrix stog ( matrix  s,
nr_complex_t  z1 = 50.0,
nr_complex_t  z2 = 50.0 
)
friend

Definition at line 1322 of file matrix.cpp.

matrix stoh ( matrix  s,
nr_complex_t  z1 = 50.0,
nr_complex_t  z2 = 50.0 
)
friend

Converts scattering parameters to hybrid matrix.

Converts chain matrix to scattering parameters Formulae are given by [5] and are remembered here:

\begin{align*} h_{11}&=\frac{(Z_{01}^*+S_{11}Z_{01}) (Z_{02}^*+S_{22}Z_{02}) -S_{12}S_{21}Z_{01}Z_{02}}{\Delta}\\ h_{12}&=\frac{2S_{12} (\Re\text{e}\;Z_{01} \Re\text{e}\;Z_{02})^\frac{1}{2}} {\Delta} \\ h_{21}&=\frac{-2S_{21} (\Re\text{e}\;Z_{01} \Re\text{e}\;Z_{02})^\frac{1}{2}} {\Delta} \\ h_{22}&=\frac{(1-S_{11})(1-S_{22})-S_{12}S_{21}}{\Delta} \end{align*}

Where $\Delta$ is:

\[ \Delta=(1-S_{11})(Z_{02}^*+S_{22}Z_{02})+S_{12}S_{21}Z_{02} \]

Bug:
{Programmed formulae are valid only for Z real}
Parameters
[in]sScattering matrix
[in]z1impedance at input 1
[in]z2impedance at input 2
Returns
hybrid matrix
Note
Assert 2 by 2 matrix
Todo:
Why not s,z1,z2 const

Definition at line 1260 of file matrix.cpp.

matrix stos ( matrix  s,
nr_complex_t  zref,
nr_complex_t  z0 = 50.0 
)
friend

S renormalization with all part identic.

Parameters
[in]soriginal S matrix
[in]zreforiginal reference impedance
[in]z0new reference impedance
Todo:
Why not inline
Returns
Renormalized scattering matrix
Todo:
s, zref and z0 const

Definition at line 901 of file matrix.cpp.

matrix stos ( matrix  s,
nr_double_t  zref,
nr_double_t  z0 = 50.0 
)
friend

S renormalization with all part identic and real.

Parameters
[in]soriginal S matrix
[in]zreforiginal reference impedance
[in]z0new reference impedance
Todo:
Why not inline
Returns
Renormalized scattering matrix
Todo:
s, zref and z0 const

Definition at line 914 of file matrix.cpp.

matrix stos ( matrix  s,
vector  zref,
nr_complex_t  z0 = 50.0 
)
friend

S renormalization (variation)

Parameters
[in]soriginal S matrix
[in]zreforiginal reference impedance
[in]z0new reference impedance
Todo:
Why not inline
Returns
Renormalized scattering matrix
Todo:
s, zref and z0 const

Definition at line 926 of file matrix.cpp.

matrix stos ( matrix  s,
nr_complex_t  zref,
vector  z0 
)
friend

S renormalization (variation)

Parameters
[in]soriginal S matrix
[in]zreforiginal reference impedance
[in]z0new reference impedance
Todo:

Why not inline

s, zref and z0 const

Returns
Renormalized scattering matrix

Definition at line 938 of file matrix.cpp.

matrix stos ( matrix  s,
vector  zref,
vector  z0 
)
friend

S params to S params.

Convert scattering parameters with the reference impedance 'zref' to scattering parameters with the reference impedance 'z0'.

Detail are given in [1], under equation (32)

New scatering matrix $S'$ is:

\[ S'=A^{-1}(S-\Gamma^+)(I-\Gamma S)^{-1}A^+ \]

Where x^+ is the adjoint (or complex tranposate) of x, I the identity matrix and $A$ is diagonal the matrix such as: $ \Gamma_i= r_i $ and $A$ the diagonal matrix such as:

\[ A_i = \frac{(1-r_i^*)\sqrt{|1-r_ir_i^*|}}{|1-r_i|} \]

Where $x*$ is the complex conjugate of $x$ and $r_i$ is wave reflexion coefficient of $Z_i'$ with respect to $Z_i^*$ (where $Z_i'$ is the new impedance and $Z_i$ is the old impedance), ie:

\[ r_i = \frac{Z_i'-Z_i}{Z_i'-Z_i^*} \]

Parameters
[in]soriginal S matrix
[in]zreforiginal reference impedance
[in]z0new reference impedance
Bug:
This formula is valid only for real z!
Todo:

Correct documentation about standing waves [1-4]

Implement Speciale implementation [2-3] if applicable

Returns
Renormalized scattering matrix
Todo:
s, zref and z0 const

Definition at line 881 of file matrix.cpp.

matrix stoy ( matrix  s,
nr_complex_t  z0 = 50.0 
)
friend

Convert scattering pto adminttance parameters identic case.

Parameters
[in]SScattering matrix
[in]z0Normalisation impedance
Returns
Admittance matrix
Todo:

Why not inline

s and z0 const

Definition at line 1092 of file matrix.cpp.

matrix stoy ( matrix  s,
vector  z0 
)
friend

Scattering parameters to admittance matrix.

Convert scattering parameters to admittance matrix. According to [1] eq (19):

\[ Z=F^{-1} (I- S)^{-1} (SG + G^+) F \]

Where $S$ is the scattering matrix, $x^+$ is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:

\begin{align*} F_i&=\frac{1}{2\sqrt{\Re\text{e}\; Z_i}} \\ G_i&=Z_i \end{align*}

Using the well know formula $(AB)^{-1}=B^{1}A^{1}$, we derivate:

\[ Y=F^{-1} (SG+G^+)^{-1} (I-S) F \]

Parameters
[in]sScattering matrix
[in]z0Normalisation impedance
Note
We could safely drop the $1/2$ in $F$ because we compute $FXF^{-1}$ and therefore $1/2$ will simplify.
Bug:
not correct if zref is complex
Todo:
s and z0 const
Returns
Admittance matrix

Definition at line 1073 of file matrix.cpp.

matrix stoz ( matrix  s,
nr_complex_t  z0 = 50.0 
)
friend

Scattering parameters to impedance matrix identic case.

Parameters
[in]sScattering matrix
[in]z0Normalisation impedance
Returns
Impedance matrix
Todo:

Why not inline?

s and z0 const?

Definition at line 983 of file matrix.cpp.

matrix stoz ( matrix  s,
vector  z0 
)
friend

Scattering parameters to impedance matrix.

Convert scattering parameters to impedance matrix. According to [1] eq (19):

\[ Z=F^{-1} (I- S)^{-1} (SG + G^+) F \]

Where $S$ is the scattering matrix, $x^+$ is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:

\begin{align*} F_i&=\frac{1}{2\sqrt{\Re\text{e}\; Z_i}} \\ G_i&=Z_i \end{align*}

Parameters
[in]sScattering matrix
[in]z0Normalisation impedance
Note
We could safely drop the $1/2$ in $F$ because we compute $FXF^{-1}$ and therefore $1/2$ will simplify.
Bug:
not correct if zref is complex
Todo:
s, z0 const
Returns
Impedance matrix

Definition at line 964 of file matrix.cpp.

matrix transpose ( matrix  a)
friend

Matrix transposition.

Parameters
[in]aMatrix to transpose
Todo:

add transpose in place

a is const

Definition at line 490 of file matrix.cpp.

matrix twoport ( matrix  m,
char  in,
char  out 
)
friend

Generic conversion matrix.

This function converts 2x2 matrices from any of the matrix forms Y, Z, H, G and A to any other. Also converts S<->(A, T, H, Y and Z) matrices. Convertion assumed:

Y->Y, Y->Z, Y->H, Y->G, Y->A, Y->S, Z->Y, Z->Z, Z->H, Z->G, Z->A, Z->S, H->Y, H->Z, H->H, H->G, H->A, H->S, G->Y, G->Z, G->H, G->G, G->A, G->S, A->Y, A->Z, A->H, A->G, A->A, A->S, S->Y, S->Z, S->H, S->G, S->A, S->S, S->T,T->T,T->S

Note
assert 2x2 matrix
Parameters
[in]mbase matrix
[in]inmatrix
[in]outmatrix
Returns
matrix given by format out
Todo:
m, in, out const

Definition at line 1585 of file matrix.cpp.

matrix ytos ( matrix  y,
nr_complex_t  z0 = 50.0 
)
friend

Convert Admittance matrix to scattering parameters identic case.

Parameters
[in]yAdmittance matrix
[in]z0Normalisation impedance
Returns
Scattering matrix
Todo:

Why not inline

y and z0 const

Definition at line 1142 of file matrix.cpp.

matrix ytos ( matrix  y,
vector  z0 
)
friend

Admittance matrix to scattering parameters.

Convert admittance matrix to scattering parameters. Using the same methodology as [1] eq (16-19), but writing (16) as $i=Yv$, ie

\[ S=F(I-G^+Y)(I-GY)^{-1}F^{-1} \]

Where $S$ is the scattering matrix, $x^+$ is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:

\begin{align*} F_i&=\frac{1}{2\sqrt{\Re\text{e}\; Z_i}} \\ G_i&=Z_i \end{align*}

Using the well know formula $(AB)^{-1}=B^{1}A^{1}$, we derivate:

\[ Y=F^{-1} (SG+G^+)^{-1} (I-S) F \]

Parameters
[in]yadmittance matrix
[in]z0Normalisation impedance
Note
We could safely drop the $1/2$ in $F$ because we compute $FXF^{-1}$ and therefore $1/2$ will simplify.
Bug:
not correct if zref is complex
Todo:
why not y and z0 const
Returns
Scattering matrix

Definition at line 1124 of file matrix.cpp.

matrix ytoz ( matrix  y)
friend

Convert admittance matrix to impedance matrix.

Convert $Y$ matrix to $Z$ matrix using well known relation $Z=Y^{-1}$

Parameters
[in]yadmittance matrix
Returns
Impedance matrix
Note
Check if y matrix is a square matrix
Todo:

Why not inline

y const

move near ztoy()

Definition at line 1371 of file matrix.cpp.

matrix ztos ( matrix  z,
nr_complex_t  z0 = 50.0 
)
friend

Convert impedance matrix to scattering parameters identic case.

Parameters
[in]ZImpedance matrix
[in]z0Normalisation impedance
Returns
Scattering matrix
Todo:

Why not inline

z and z0 const

Definition at line 1028 of file matrix.cpp.

matrix ztos ( matrix  z,
vector  z0 
)
friend

Convert impedance matrix scattering parameters.

Convert scattering parameters to impedance matrix. According to [1] eq (18):

\[ S=F(Z-G^+)(Z+G)^{-1} F^{-1} \]

Where $Z$ is the scattering matrix, $x^+$ is the adjoint of x, I the identity matrix. The matrix F and G are diagonal matrix defined by:

\begin{align*} F_i&=\frac{1}{2\sqrt{\Re\text{e}\; Z_i}} \\ G_i&=Z_i \end{align*}

Parameters
[in]ZImpedance matrix
[in]z0Normalisation impedance
Returns
Scattering matrix
Note
We could safely drop the $1/2$ in $F$ because we compute $FXF^{-1}$ and therefore $1/2$ will simplify.
Bug:
not correct if zref is complex
Todo:
z and z0 const?

Definition at line 1009 of file matrix.cpp.

matrix ztoy ( matrix  z)
friend

impedance matrix to admittance matrix.

Convert impedance matrix to admittance matrix. By definition $Y=Z^{-1}$

Parameters
[in]zimpedance matrix
Returns
Admittance matrix
Todo:

Why not inline

z const

Definition at line 1041 of file matrix.cpp.

The documentation for this class was generated from the following files:
Generated on Tue Dec 25 2012 14:32:00 for My Project by   doxygen 1.8.2