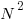1 4 9 16 25 36 49 ….
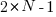1 3 5 7 9 11 13
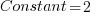2 2 2 2 2 2
![N^2 = sum{i=1}{N}{delim{[}{ 2i - 1 }{]}}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_975_a1729111b547d0654d2cbc30b583cfed.png "N^2 = sum{i=1}{N}{delim{[}{ 2i - 1 }{]}}")
For example:
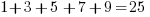
And it is interesting to note that 9 is an integer square all by itself so
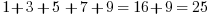or
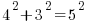
Which is an integer solution of Pythagorean relation. Its easy to see that that right hand side must be an odd number in this case of a single term of the summation being a perfect square. Of course this changes when you ask that 2 terms sum up to a perfect square.
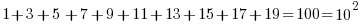
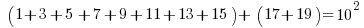or 
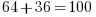which is
It appears from this point of view that the numbers in both sets must be from a contiguous series or the sum of the set will go off the perfect square grid. If you remove the sequence of the smaller square from a bigger square all that is left is the higher terms and no way of swapping any terms to get the same answer.
Pythagorean Triples in Wikipedia
Fermats last theorem states that there are no integer solutions for
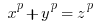where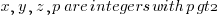 
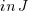
The point of view above can be used to illustrate a good view of why. I will use the perfect cubes to illustrate
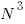1 8 27 64 125 216 343 512 729 1000
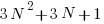1 7 19 37 61 91 127 169
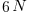6 12 18 24 30 36 42
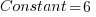6 6 6 6 6 6
![N^3 = sum{i=1}{N}{delim{[}{ 3i^2 + 3i + 1 }{]}}](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_972_41f9590964fed9a6373e9042d84495a2.png "N^3 = sum{i=1}{N}{delim{[}{ 3i^2 + 3i + 1 }{]}}")
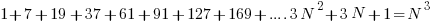
In the first situation the summed term simply incremented by 2 each time and was bound to hit on perfect integer squares. In this example the term really starts moving along and is much less likely to encounter a perfect cube. In fact we know it to never encounter one. It only gets worse at higher integer exponents.
Links
2 Comments
Dang, it looks like you could extend that analysis into a few page proof of Fermat's Last Theorm, thus making Andrew Wiles cry! he spent 7 years to do it…
I find it interesting that the gov’t can look at our bits and pieces (via TSA), but WikiLeaks can’t do the same to the gov’t.