Show that the curve:
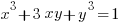
contains only one set of three distinct points, A, B, and C, which are vertices of an equilateral triangle, and find its area.
The “curve”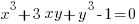 
is actually reducible, because the left side factors as
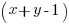Moreover, the second factor is
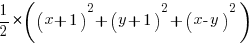
so it only vanishes at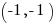 
. Thus the curve in question consists of the single point 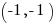together with the line
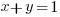
To form a triangle with three points on this curve, one of its vertices must be 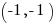. The other two vertices lie on the line 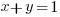so the length of the altitude from 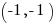is the distance from 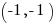to 
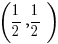or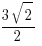 
The area of an equilateral triangle of height h is 
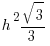, so the desired area is 
.
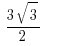Remark:
The factorization used above is a special case of the fact that
.
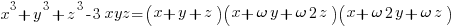Where omega denotes a primitive cube root of unity. That fact in turn follows from the evaluation of the determinant of the circulant matrix
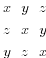
by reading off the eigenvalues of the eigenvectors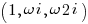 
for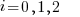 
1 Comment
Bagus Buuuuuuuuuuuuaaaaaaaaaaaaaaaaaaaaaannnnnnnnnnnnnnnnnnnnnggggggggggggggeeeeeeeeeeeetttttttttttttt DEH DEH DEH DEH !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!