RSA Code Made Easy

A code is implemented with the following statement.  Decrypt the code.

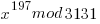
The totient of 3131 is needed and is found below:

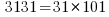
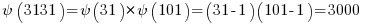       because 31 and 101 are prime

Eulers Theorem: 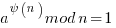   so:

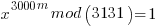       Where m is an integer to give us more flexibility in generating an inverse in step XXX below.   Multiply both sides by x

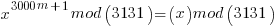
So if you can find a power d where:

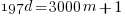     or equivalently:

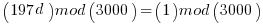    then you can take the encrypted numbers to the power of d and out will pop the plain text original series

Now you use the Euclidean algorithm to find 1 in terms of 197 and 3000. This yields:

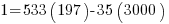       Taking the mod(3000) of both sides

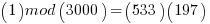    which shows  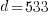is the decryption power we are looking for

This example used smaller numbers so as to make the example transparent.  However if the input character were to be X=31 or 101 I think the system breaks down.