MOSFET Slope Factor n

â€‹

${C_D/C_ox}={varepsilon_S}/{t_D} {/} {varepsilon_ox}/{t_ox}$

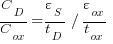
Definition of n is:

${n}= 1 + {C_D/C_ox}$

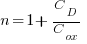
Substituting:

${n}= 1 +{varepsilon_S}/{x_D} {/} {varepsilon_ox}/{t_ox}$

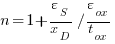
Using the depletion width from table:

${n}= 1 +{varepsilon_S}/{sqrt { {2 phi_s } / {Phi_s}}} {/} {varepsilon_ox}/{t_ox}$

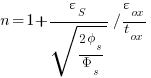
Which can be simplified quickly to the following when needed:

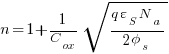${n}= 1 + 1/{C_ox} {sqrt{ {q{varepsilon_S}{N_a}}/{2 phi_s} } }$ ….this is almost the same as equation 2.1.58 of CMOS Analog Design Using All Region MOSFET Modeling

If you want to include the linear term of depletion region electric field then substitute 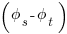${(phi_s - phi_t)}$ for ${phi_s}$

${n}= 1 + 1/{C_ox} {sqrt{ {q{varepsilon_S}{N_a}} / {2 (phi_s - phi_t)} } }$

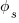
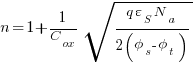
And the phrase now exactly matches the book.

Identity Table

$Phi = {qN_a / varepsilon_s}$	$E_surface = sqrt { {2 phi_s Phi_s} }$
$x_d = sqrt { {2 phi_s } / {Phi_s} }$
${C_D/C_ox}={varepsilon_S}/{t_D} {/} {varepsilon_ox}/{t_ox}$	$gamma = {varepsilon_s}/{1} {/} {varepsilon_ox}/{t_ox} {sqrt{2 Phi_s }}$

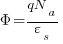
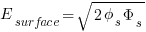
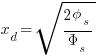
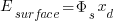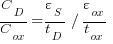
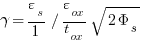
Research Links