Added 9-30-2024: Why the symmetry at 25?
I wondered why the symmetry at N=25. For this you look at
![[( 10d2 + d1 )^2 ]mod_10 [( 10d2 + d1 )^2 ]mod_10](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981.5_dd3b2c51b55901af8cd08a8cd2f75482.png)
This is what you see in the excel table around N=25.
Walking the beira mar here in Sao Jose, SC. Keeping my mind busy during the fake virus scare / Bank Robbery. This entire entry is about what I am learning from calculating the squares of the numbers 0 through 100 mentally as I walk the beira mar. First thing you see is that the lowest 2 digits are limited in their values and cyclical.
The last two digits are only unique up to 24. The numbers are:

|
Last two digits of perfect squares
|
It is interesting to note that all polynomials are periodic at maximum in the modulus number. However in the above graph you see two full cycles in the span of the modulus of 100. This lead me to investigate the conditions under which 2 cycles occur.
![N^2 Mod M = [ N - M/2 ]^2 Mod M N^2 Mod M = [ N - M/2 ]^2 Mod M](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_92ccc057cd5b37a1fe85ed540976523f.png)
![N^2 Mod M = [ N^2 - MN + M^2 / 2^2 ] Mod M N^2 Mod M = [ N^2 - MN + M^2 / 2^2 ] Mod M](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_978_2768cfbbe3deef3d8c37c45a22ae1f03.png)
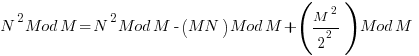
Thus 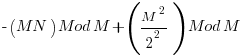 must equal zero
must equal zero
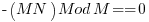 identically
identically
and thus the condition for 2 full cycles in M integers is
 <— I have problems reducing these forms of modulus with divisors other than brute force: there is a bit of a gap between here and the next step which needs filled for this procedure to be generalized.
<— I have problems reducing these forms of modulus with divisors other than brute force: there is a bit of a gap between here and the next step which needs filled for this procedure to be generalized.
This means the requirement for 2 cycles in M integers is that M must have a factor of 4 in it. The values M=….100,80,60,40…..all have double periodicity.
Setting M=4 yields

Which shows that a perfect square must be: 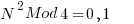
A natural subsequent question is if 3x periodicity is possible. For that we have
![N^2 Mod M = [ N - M/3 ]^2 Mod M N^2 Mod M = [ N - M/3 ]^2 Mod M](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_1bb0ddc8fc7dbee1c78aa84e3a628098.png)
![N^2 Mod M = [ N^2 - (2/3)MN + M^2 / 3^2 ] Mod M N^2 Mod M = [ N^2 - (2/3)MN + M^2 / 3^2 ] Mod M](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_978_15a68ae4c5d7fdb9b35b3bf2909db7f4.png) removing the like terms from both sides
removing the like terms from both sides
![0 = [ - (2/3)MN + M^2 / 3^2 ] Mod M 0 = [ - (2/3)MN + M^2 / 3^2 ] Mod M](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_978_2a505cb0f98616ff0495607fe20d53fe.png) The problem here is that if we choose M=90 for instance so the second term's modulus = 0 then the first term is
The problem here is that if we choose M=90 for instance so the second term's modulus = 0 then the first term is
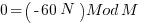
Which with N the running variable it is not always equal to zero. Thus it appears 3 cycles within the M cyclicity is ruled out. In fact if you look carefully it appears only 2 cycles are possible within the M periodicity because the same term that threw a wrench in the works spoils all others. It appears the reason this works for cyclicity = 2 is that the coefficient of a square polynomial cancels out the fraction in the 1st order term and thus is only available or this cyclicity.
Observations
- Where ever you place a tangent line on the parabola the displacement from the tangent line has the basic parabola ….16,9,4,1,0,1,4,9,16…. around the tangent point. You can see this in the table below and it is used to ease the task of memorization. This is easiest to see around the "lines of symmetry".
On the memorization of the square of 0 – 100
-
a=Atom means you have to memorize – you can start by using the (x-y)(x+y) trick. Ex:
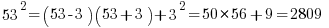 , These are the unique last 2 digits of perfect squares.
, These are the unique last 2 digits of perfect squares.
- ap= atomic prime – means you can use an atomic to calculate it but soon you will be rattling it off from memory
- Jump == hundreds digit jump
- L.O.S. == Line of Symmetry
| Int_ | Type | Jump | Square | Step | L.O.S. |
| 00 | a | 0000 | |||
| 01 | a | 0001 | |||
| 02 | a | 0004 | |||
| 03 | a | 0009 | |||
| 04 | a | 0016 | |||
| 05 | a | 0025 | |||
| 06 | a | 0036 | |||
| 07 | a | 0049 | |||
| 08 | a | 0064 | |||
| 09 | a | 0081 | |||
| 10 | a | 0100 | |||
| 11 | a | 0121 | |||
| 12 | a | 0144 | |||
| 13 | a | 0169 | |||
| 14 | a | 0196 | |||
| 15 | a | 0225 | |||
| 16 | a | 0256 | |||
| 17 | a | 0289 | |||
| 18 | a | 0324 | |||
| 19 | a | 0361 | |||
| 20 | a | 0400 | |||
| 21 | a | 0441 | |||
| 22 | a | 0484 | |||
| 23 | a | 0529 | |||
| 24 | a | 0576 | |||
| 25 | a | 0625 | 1st | ||
| 26 | ap | 0676 | 576+100 | ||
| 27 | ap | 0729 | 529+200 | ||
| 28 | ap | 0784 | 484+300 | ||
| 29 | ap | 0841 | 441+400 | ||
| 30 | ap | 0900 | 400+500 | ||
| 31 | ap | 0961 | 361+600 | ||
| 32 | ap | 1024 | 324+700 | ||
| 33 | ap | 1089 | 289+800 | ||
| 34 | ap | 1156 | 256+900 | ||
| 35 | ap | 1225 | 225+1000 | ||
| 36 | ap | 1296 | 196+1100 | ||
| 37 | ap | 1369 | 169+1200 | ||
| 38 | ap | 1444 | 144+1300 | ||
| 39 | ap | 1521 | 121+1400 | ||
| 40 | ap | 1600 | 100+1500 | ||
| 41 | 1681 | 1600+81 | |||
| 42 | 100 | 1764 | 1700+64 | ||
| 43 | 100 | 1849 | 1800+49 | ||
| 44 | 100 | 1936 | 1900+36 | ||
| 45 | 100 | 2025 | 2000+25 | ||
| 46 | 100 | 2116 | 2100+16 | ||
| 47 | 100 | 2209 | 2200+09 | ||
| 48 | 100 | 2304 | 2300+04 | ||
| 49 | 100 | 2401 | 2400+01 | ||
| 50 | 100 | 2500 | 2500+00 | 2nd | |
| 51 | 100 | 2601 | 2600+01 | ||
| 52 | 100 | 2704 | 2700+04 | ||
| 53 | 100 | 2809 | 2800+09 | ||
| 54 | 100 | 2916 | 2900+16 | ||
| 55 | 100 | 3025 | 3000+25 | ||
| 56 | 100 | 3136 | 3100+36 | ||
| 57 | 100 | 3249 | 3200+49 | ||
| 58 | 100 | 3364 | 3300+64 | ||
| 59 | 100 | 3481 | 3400+81 | ||
| 60 | 100 | 3600 | 3500+100 | ||
| 61 | 100 | 3721 | 3600+121 | ||
| 62 | 100 | 3844 | 3700+144 | ||
| 63 | 100 | 3969 | 3800+169 | ||
| 64 | 100 | 4096 | 3900+196 | ||
| 65 | 200 | 4225 | 4000+225 | ||
| 66 | 100 | 4356 | 4100+256 | ||
| 67 | 100 | 4489 | 4200+289 | ||
| 68 | 200 | 4624 | 4300+324 | ||
| 69 | 100 | 4761 | 4400+361 | ||
| 70 | 200 | 4900 | 4500+400 | ||
| 71 | 100 | 5041 | 4600+441 | ||
| 72 | 100 | 5184 | 4700+484 | ||
| 73 | 200 | 5329 | 4800+529 | ||
| 74 | 100 | 5476 | 4900+576 | ||
| 75 | 200 | 5625 | 5000+625 | 3rd | |
| 76 | 100 | 5776 | 5100+676 | ||
| 77 | 200 | 5929 | 5200+729 | ||
| 78 | 100 | 6084 | 5300+784 | ||
| 79 | 200 | 6261 | 5400+841 | ||
| 80 | 200 | 6400 | 5500+900 | ||
| 81 | 100 | 6561 | 5600+961 | ||
| 82 | 200 | 6724 | 5700+1024 | ||
| 83 | 100 | 6889 | 5800+1089 | ||
| 84 | 200 | 7056 | 5900+1156 | ||
| 85 | 200 | 7225 | 6000+1225 | ||
| 86 | 100 | 7396 | 6100+1296 | ||
| 87 | 200 | 7569 | 6200+1369 | ||
| 88 | 200 | 7744 | 6300+1444 | ||
| 89 | 200 | 7921 | 6400+1521 | ||
| 90 | 200 | 8100 | 6500+1600 | ||
| 91 | 200 | 8281 | 8200+81 | ||
| 92 | 200 | 8464 | 8400+64 | ||
| 93 | 200 | 8649 | 8600+49 | ||
| 94 | 200 | 8836 | 8800+36 | ||
| 95 | 200 | 9025 | 9000+25 | ||
| 96 | 200 | 9216 | 9200+16 | ||
| 97 | 200 | 9409 | 9400+09 | ||
| 98 | 200 | 9604 | 9600+04 | ||
| 99 | 200 | 9801 | 9800+01 | ||
| 100 | 200 | 10000 | 10000+00 |
Graph of 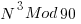
The above graph is the cube of the first 100 integers with the modulus selected to give 3 cycles over the mod 100 cycle. Looking at the form
![[ N + M ]^3 = N^3 + 3N^2 M + 3N M^2 + N^3 [ N + M ]^3 = N^3 + 3N^2 M + 3N M^2 + N^3](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_3113c6402cc97e33d4376987fd5cb717.png)
Seeing this form it is apparent that 3 cycles can be realized within the modulus cycle with the correct choice of modulus. Setting:
![N^3 Mod M = [ N + M/3 ]^3 Mod M N^3 Mod M = [ N + M/3 ]^3 Mod M](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_0af36237094f464bc367fd0cc3b654d6.png)
Expanding
![N^3 Mod M = [ N^3 + 3N^2 M + 3N M^2/3^2 + M^3/3^3 ] Mod M N^3 Mod M = [ N^3 + 3N^2 M + 3N M^2/3^2 + M^3/3^3 ] Mod M](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_978_57c8a2308379104ede2c2ed5219fbc53.png)

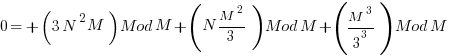
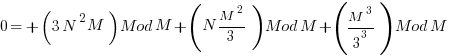
- The first term is obviously 0 under all conditions.
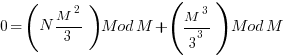
- The 2nd and 3rd term can be engineered by picking M to make them always zero. The minimum value that works is 9 which you can see by playing with substituting numbers and looking at the resulting terms of the modulus.
Setting M=9 shows:

Which shows that a perfect cube must be: 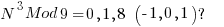
In the mathematics of sums of powers, it is an open problem to characterize the numbers that can be expressed as a sum of three cubes of integers, allowing both positive and negative cubes in the sum. A necessary condition for {\displaystyle n} to equal such a sum is that {\displaystyle n} cannot equal 4 or 5 modulo 9, because the cubes modulo 9 are 0, 1, and −1, and no three of these numbers can sum to 4 or 5 modulo 9.[1] It is unknown whether this necessary condition is sufficient. See: Wikipedia: Sums of three cubes
First 3 Digits of Integer Squares



 to equal such a sum is that {\displaystyle n}
to equal such a sum is that {\displaystyle n}
0 Comments