Farmer buys livestock puzzle

A farmer has 100 dollars to buy 100 animals.  A cow costs 10, a pig costs 5 and a chicken costs 50 cents.  How many of each does he buy?  He must use all his money and he must buy at least 1 of each type.

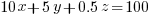
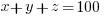
note Z must be even because otherwise you will get  ddd.5<> 100 in the first equation. Eliminate z by multiplying first equation by 2 and subtracting the second equation

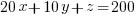
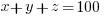
yields

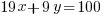 Here a solution is only found because the solution is specified to be integers

 

Brute force Integer solution

Find a solution for the above and plugging into: 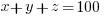   now plug in number until you get an even z. Try x=1:

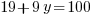
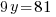
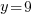
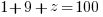
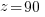
and is even and thus the problem is done

 

Modulus Solution

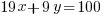
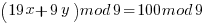
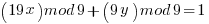
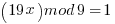
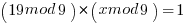
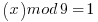
Two obvious solutions are 

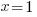 and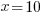   

The first solution is viable.  The second is not because there is no money left over to buy any other type of animal.