Research Links
- Wikipedia: Eulers Theorem
- Wikipedia Euler Totient Function
- Online totient calculator
- Euler's theorem derivation
- Fermat's little theorem
Eulers theorem is very similar to Fermat's little theorem. It is not restricted to prime number p. It is restricted to relatively prime a & p. It states:
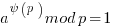
Where 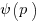 is the Euler totient function which is the number of integers less than and coprime to p.
is the Euler totient function which is the number of integers less than and coprime to p.
Example:
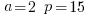
List of relative primes for ![15 = [ 1, 2, 4, 7, 8, 11,13, 14 ] 15 = [ 1, 2, 4, 7, 8, 11,13, 14 ]](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981.5_0f791810f8a7c84a44f8985bc46d4aec.png) thus
thus 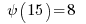
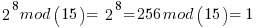
If you followed the proof for Fermat's little theorem then you can understand this generalization rapidly. As before when the integer a is coprime to p you get the jumble of all the integers 1,2,3…p-1. This was guaranteed by p being prime in Fermat's little theorem. When you relent on that condition then you have some integers a that are not coprime to p and they will not give you a full contingent of integers. See the spread sheet clips below
2 is coprime to 15 and thus all values 0 through 14 are cycled through. 3 is not coprime to 15 and thus the gearing does not cycle through all values.
In the spread sheet example clipped above the totient 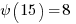
The following spread sheet snip contains the value of the modulus 1 to p-1 where p=15 in this case and the modulus of a*remainder. As before with Fermat's little theorem the modulus values come in different order but contain identical values.

Thus:
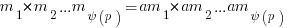
![m_1 * m_2 ...m_{psi(p)} = a^{psi(p)}*[ m_1 * m_2 ...m_{psi(p)}] mod p m_1 * m_2 ...m_{psi(p)} = a^{psi(p)}*[ m_1 * m_2 ...m_{psi(p)}] mod p](https://www.amarketplaceofideas.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981.5_c113c4914e59496cad13db65739b377c.png)
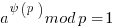
Above needs work. See video derivation


0 Comments