Research Links
- Fermat–Euler theorem
- Euler's totient function
- Fermat's little theorem
- Proofs of Fermat's little theorem
- Proof of Fermat's Little Theorem
- Chinese remainder theorem
- Eulers Theorem – a more general version that only specifies coprime requirement instead of prime requirement.
Fermat's little theorem states that if p is a prime number, then for any integer a, the number a p − a is an integer multiple of p. In the notation of modular arithmetic, this is expressed as
For example, if a = 2 and p = 7, 27 = 128, and 128 − 2 = 7 × 18 is an integer multiple of 7.
If a is not divisible by p, Fermat's little theorem is equivalent to the statement that a p − 1 − 1 is an integer multiple of p:
The following table has a = 3 with p=17. Notice how the result Mod(in) has every number 1 through 16 exactly 1 time each. I call this disordered sequential list a "jumble". This can be used to generate a quick intuitive derivation of the theorem.

Multiply each row together to get:
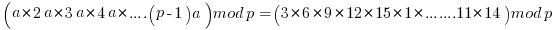
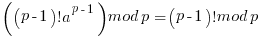
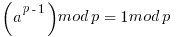
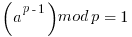
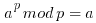
It is in the above paragraph of mathematics that you can see that all the numbers 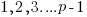 must be relatively prime to p in order for the derivation to work and the relation to hold. If not some of the values in the jumble will be skipped.
must be relatively prime to p in order for the derivation to work and the relation to hold. If not some of the values in the jumble will be skipped.
??????? Not sure what I saw below
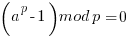 Below is an example of the values of this phrase with p=5
Below is an example of the values of this phrase with p=5

Fermat's Little Theorem Spreadsheet
Observation: Relationship of the Roots of the Polynomial
Using the example 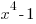 assuming p=5 you get the following root map:
assuming p=5 you get the following root map:

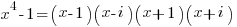
for x=2:
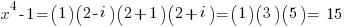 and this relationship works for all the coprimes.
and this relationship works for all the coprimes.
for x=3:
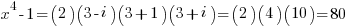
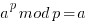
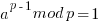
0 Comments