Research Links
- Google: diophantine equation pythagoras
- Chapter 1: DIOPHANTINE ANALYSIS – UnKnown Book
- Diophantine Equations – Chapter 5 – Diophantine Analysis monograph by Robert Daniel Carmichael
Pythagorean Triples Solution
The square of the odd number
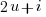 is
is 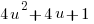
Hence the sum of two odd squares is divisible by 2 but not by 4; and therefore the sum of two odd squares cannot be a square. Hence of the numbers x, y one is even. If we suppose that y is even, then x and z are both odd.
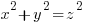
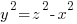
Both x and z terms in the parenthesis below will be odd and thus the sum and difference will be even
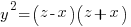
Every common divisor of 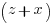 and
and 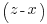 is a divisor of their difference 2x. Thence, since z and x are relatively prime odd numbers we conclude that 2 is the greatest common divisor of
is a divisor of their difference 2x. Thence, since z and x are relatively prime odd numbers we conclude that 2 is the greatest common divisor of 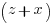 and
and 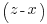 . Then we see that each of these numbers must be twice a square, so that we may write
. Then we see that each of these numbers must be twice a square, so that we may write
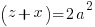
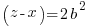
Solving for x, y, z yields
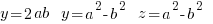
Using values of a & b you can generate all the integer solutions.
A variant on the above can be done to illustrate the solution technique more
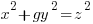
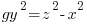
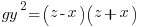 Using the same argument as above but one of the factors on the right hand side has to account for the g. Since the g can be in either factor there are two solutions that make up the overall solution
Using the same argument as above but one of the factors on the right hand side has to account for the g. Since the g can be in either factor there are two solutions that make up the overall solution
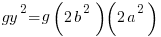 Matching the previous phrase with this phrase to equate right hand factor terms
Matching the previous phrase with this phrase to equate right hand factor terms
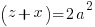
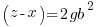 —-OR—-
—-OR—- 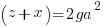
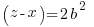
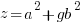
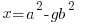 —-OR—-
—-OR—- 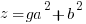
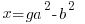
| Example Solutions with g=2 a=4 b=1 | |||
| x | y | z | Equation Set |
| 2 | 4 | 6 |
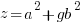 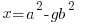
|
| 7 | 4 | 9 |
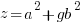 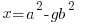
|
0 Comments