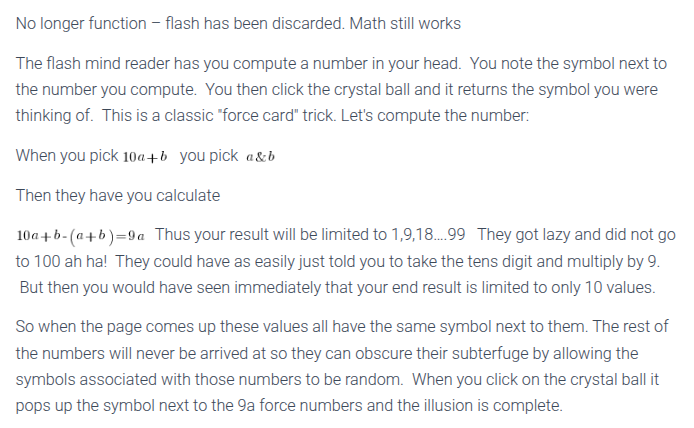
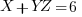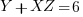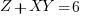Euclidean Algorithm for Greatest Common Denominator
Research Links Wikipedia: Euclidean algorithm A 24-by-60 rectangle is covered with ten 12-by-12 square tiles, where 12 is the GCD of 24 and 60. More generally, an a-by-b rectangle can be covered with square tiles of side-length c only if c is a common divisor of a and b. So the task is to find the largest square that tiles Read more…
Eulers Theorem
If you followed the proof for Fermat's little theorem then you can understand this generalization rapidly. As before when the integer a is coprime to p you get the jumble of all the integers 1,2,3…p-1. This was guaranteed by p being prime in Fermat's little theorem. When you relent on that condition then you have some integers a that are not coprime to p and they will not give you a full contingent of integers. See the spread sheet clips below
2 is coprime to 15 and thus all values 0 through 14 are cycled through. 3 is not coprime to 15 and thus the gearing does not cycle through all values.
Euler Fermat Theorem – Fermats Little Theorem
Research Links
- Fermat–Euler theorem
- Euler's totient function
- Fermat's little theorem
- Proofs of Fermat's little theorem
- Proof of Fermat's Little Theorem
- Chinese remainder theorem
- Eulers Theorem – a more general version that only specifies coprime requirement instead of prime requirement.