Integer Square 1 to 100

Added 9-30-2024:  Why the symmetry at 25?

I wondered why the symmetry at N=25. For this you look at

This is what you see in the excel table around N=25.

Excel File here

 

 

 

Walking the beira mar here in Sao Jose, SC. Keeping my mind busy during the fake virus scare / Bank Robbery.   This entire entry is about what I am learning from calculating the squares of the numbers 0 through 100 mentally as I walk the beira mar.  First thing you see is that the lowest 2 digits are limited in their values and cyclical. 

  The last two digits are only unique up to 24. The numbers are:

Last two digits of perfect squares Integer x^2 Mod(100) Integer 00 00 50 01 01 49 02 04 48 03 09 47 04 16 46 05 25 45 06 36 44 07 49 43 08 64 42 09 81 41 10 00 40 11 21 39 12 44 38 13 69 37 14 96 36 15 25 35 16 56 34 17 89 33 18 24 32 19 61 31 20 00 30 21 41 29 22 84 28 23 29 27 24 76 26 25 25

It is interesting to note that all polynomials are periodic at maximum in the modulus number.  However in the above graph you see two full cycles in the span of the modulus of 100.  This lead me to investigate the conditions under which 2 cycles occur. 

  

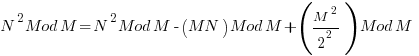
Thus 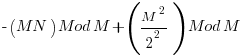   must equal zero

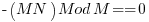    identically 

and thus the condition for 2 full cycles in M integers is   

       <— I have problems reducing these forms of modulus with divisors other than brute force: there is a bit of a gap between here and the next step which needs filled for this procedure to be generalized.

 This means the requirement for 2 cycles in M integers is that M must have a factor of 4 in it. The values  M=….100,80,60,40…..all have double periodicity.

Setting M=4 yields

Which shows that a perfect square must be: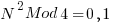  

---

A natural subsequent question is if 3x periodicity is possible. For that we have

   removing the like terms from both sides

    The problem here is that if we choose M=90 for instance so the second term's modulus = 0 then the first term is 

 

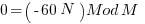
Which with N the running variable it is not always equal to zero.  Thus it appears 3 cycles within the M cyclicity is ruled out.  In fact if you look carefully it appears only 2 cycles are possible within the M periodicity because the same term that threw a wrench in the works spoils all others.  It appears the reason this works for cyclicity = 2 is that the coefficient of a square polynomial cancels out the fraction in the 1st order term and thus is only available or this cyclicity.

---

Observations 

• Where ever you place a tangent line on the parabola the displacement from the tangent line has the basic parabola ….16,9,4,1,0,1,4,9,16…. around the tangent point.  You can see this in the table below and it is used to ease the task of memorization.  This is easiest to see around the "lines of symmetry".

On the memorization of the square of 0 – 100

• a=Atom means you have to memorize – you can start by using the (x-y)(x+y) trick. Ex: 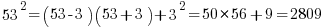 ,   These are the unique last 2 digits of perfect squares.
• ap= atomic prime – means you can use an atomic to calculate it but soon you will be rattling it off from memory
• Jump == hundreds digit jump
• L.O.S. == Line of Symmetry

Int_	Type	Jump	Square	Step	L.O.S.
00	a		0000
01	a		0001
02	a		0004
03	a		0009
04	a		0016
05	a		0025
06	a		0036
07	a		0049
08	a		0064
09	a		0081
10	a		0100
11	a		0121
12	a		0144
13	a		0169
14	a		0196
15	a		0225
16	a		0256
17	a		0289
18	a		0324
19	a		0361
20	a		0400
21	a		0441
22	a		0484
23	a		0529
24	a		0576
25	a		0625		1st
26	ap		0676	576+100
27	ap		0729	529+200
28	ap		0784	484+300
29	ap		0841	441+400
30	ap		0900	400+500
31	ap		0961	361+600
32	ap		1024	324+700
33	ap		1089	289+800
34	ap		1156	256+900
35	ap		1225	225+1000
36	ap		1296	196+1100
37	ap		1369	169+1200
38	ap		1444	144+1300
39	ap		1521	121+1400
40	ap		1600	100+1500
41			1681	1600+81
42		100	1764	1700+64
43		100	1849	1800+49
44		100	1936	1900+36
45		100	2025	2000+25
46		100	2116	2100+16
47		100	2209	2200+09
48		100	2304	2300+04
49		100	2401	2400+01
50		100	2500	2500+00	2nd
51		100	2601	2600+01
52		100	2704	2700+04
53		100	2809	2800+09
54		100	2916	2900+16
55		100	3025	3000+25
56		100	3136	3100+36
57		100	3249	3200+49
58		100	3364	3300+64
59		100	3481	3400+81
60		100	3600	3500+100
61		100	3721	3600+121
62		100	3844	3700+144
63		100	3969	3800+169
64		100	4096	3900+196
65		200	4225	4000+225
66		100	4356	4100+256
67		100	4489	4200+289
68		200	4624	4300+324
69		100	4761	4400+361
70		200	4900	4500+400
71		100	5041	4600+441
72		100	5184	4700+484
73		200	5329	4800+529
74		100	5476	4900+576
75		200	5625	5000+625	3rd
76		100	5776	5100+676
77		200	5929	5200+729
78		100	6084	5300+784
79		200	6261	5400+841
80		200	6400	5500+900
81		100	6561	5600+961
82		200	6724	5700+1024
83		100	6889	5800+1089
84		200	7056	5900+1156
85		200	7225	6000+1225
86		100	7396	6100+1296
87		200	7569	6200+1369
88		200	7744	6300+1444
89		200	7921	6400+1521
90		200	8100	6500+1600
91		200	8281	8200+81
92		200	8464	8400+64
93		200	8649	8600+49
94		200	8836	8800+36
95		200	9025	9000+25
96		200	9216	9200+16
97		200	9409	9400+09
98		200	9604	9600+04
99		200	9801	9800+01
100		200	10000	10000+00

---

Graph of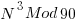    

 

The above graph is the cube of the first 100 integers with the modulus selected to give 3 cycles over the mod 100 cycle.  Looking at the form

 

Seeing this form it is apparent that 3 cycles can be realized within the modulus cycle with the correct choice of modulus.  Setting:

  

Expanding

  

  

  

  

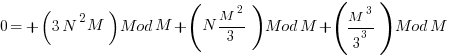
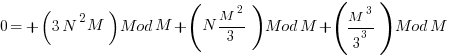
• The first term is obviously 0 under all conditions.

  

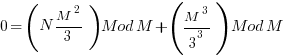
• The 2nd and 3rd term can be engineered by picking M to make them always zero.  The minimum value that works is 9 which you can see by playing with substituting numbers and looking at the resulting terms of the modulus.

 

Setting M=9 shows:

Which shows that a perfect cube must be: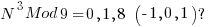  

In the mathematics of sums of powers, it is an open problem to characterize the numbers that can be expressed as a sum of three cubes of integers, allowing both positive and negative cubes in the sum. A necessary condition for {\displaystyle n} to equal such a sum is that {\displaystyle n} cannot equal 4 or 5 modulo 9, because the cubes modulo 9 are 0, 1, and −1, and no three of these numbers can sum to 4 or 5 modulo 9.^[1] It is unknown whether this necessary condition is sufficient.   See: Wikipedia: Sums of three cubes

 

First 3 Digits of Integer Squares

• http://www.amarketplaceofideas.com/wp-content/uploads/2020/05/Squares-Cyclicity-1-500.xls