Research Links
The clerks attached to the finn of Pilkins and Popinjay arranged that three of them would lunch together every day at a particular table so long as they could avoid the same three men sitting down twice together. The same number of clerks of Messrs. Radson, Robson, and Ross decided to do precisely the same, only with four men at a time instead of three. On working it out they found that Radson's staff could keep it up exactly three times as many
days as their neighbors. What is the least number of men there could have been in each staff?
Number of staff both companies: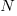 
Company P&P number of permissible ways to select 3 staff for lunch: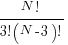 
Company R&R number of permissible ways to select 3 staff for lunch: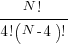 
We are given second phrase is 3x the first phrase
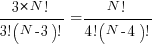
Rearranging yields
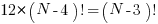
It is relatively easy to see the only way this equation holds is if the right hand set of parenthesis holds the value 12 and thus
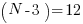yielding
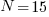
You can see the mathematical easter egg in this problem that allowed for a nice neat integerial solution is fhe rigged factor of 3 with the increment of 1 in group size.
0 Comments