536 Puzzles: Problem & Solution #1: Concerning a Check

A man went into a bank to cash a check. In handing over the money the cashier, by mistake, gave him dollars for cents and cents for dollars. He pocketed the money without examining it, and spent a nickel on his way home. He then found that he possessed exactly twice the amount of the check. He had no money in his pocket before going to the bank. What was the exact amount of that check?

Excel Spreadsheet method

• The first sheet uses a brute force method of stepping through all the values from 00.00 to 99.99 and looking for an integer solution
• The second sheet uses the relation below to drive towards a less brute force method
• The third sheet of the spread sheet shows how the solution is periodic like a set of gears.  The constant term added is represented as the column offset number and is analogous to a number of teeth offset from zero position at the start of turning of the gears.
• The fourth sheet uses 5 and 7 to simplify the problem 

 

Second Sheet Method

Assume a form of the check 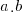.  Where a is the dollar amount and b the cents.

Thus the relation detailed in the puzzle can be written

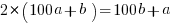
rearranging terms

 

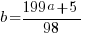
Using this you can look for an integer solution using less brute force and this is depicted on the second page of the spreadsheet.

 

Third Sheet – Depiction of the numbers as gearing

           

The right hand image shows gear foot print with no offset and with an offset of 1 tooth.  The modulus showing up in number of teeth out of both gears being at an integer number of turns.   The initial offset=0 7t mod(5) [pmath] sequence is 2,4,1,3,0.  The initial offset [pmath] 7t mod(5) [pmath] sequence is 3,0,2,4,1. Both sequence through all values up to p-1 which is 4 in this case.  It’s obvious in order to return to the initial starting position from the offset=1 condition requires 2 turns of the 7-gear.     this corresponds to advancing the gear teeth marker 1 tooth 

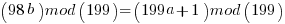   and since a is to be an integer solution:

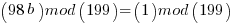
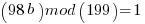 and thus b will be the modulo multiplicative inverse of 98 in mod 199.  Online calculator here.

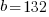 so with 1 tooth of advancement it will require only 132 rotations of the big gear for the dots come back into alignment.  Using this offset 5 times will lead to  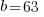and from this we calculate  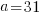This method eliminates all the brute force methodology.  

 

Diophantine Equation Approach

Next a solution via the linear Diophantine equation approach.  The equation to solve is: 

• -199x + 98y = 5

Calculating GCD(-199,98) gives:

98 = (0)*(-199) + 98

-199 = (-3)*98 + 95

98 = 1*95 + 3

95 = 31*3 + 2

3 = 1*2 + 1

2 = 2*1 + 0

Then applying the Extended Euclidean Algorithm:

1	=	(1 * 3) + (-1 * 2)
	=	(-1 * 95) + (32 * 3)
	=	(32 * 98) + (-33 * 95)
	=	(-33 * -199) + (-67 * 98)
	=	(-67 * 98) + (-33 * -199)

The complete solution is:

x = -165 + 98n y = -335 + 199n

With 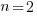you arrive at the solution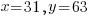 

Research Links

• Modular multiplicative inverse
• Extended Euclidean algorithm 
• Extended Euclidean algorithm
• Linear Diophantine Equation Solver
• 536 Puzzles and Curious Problems