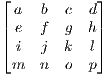
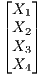 =
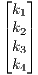
=
.In the following I deviate from standard matrix element notation because it is hard to differentiate terms that only use different subscript.
.
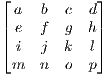
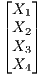 =
=
In the following I will not include the equations right side since we already know what happens there from the 3x3 case previously presented
We will use first step of Gaussian elimination to reduce the problem to a 3x3 determinant. The steps are:
After these steps the matrix looks is:

What remains for Gaussian reduction includes the upper left 3x3 of the matrix. The vertical bars denote 2x2 determinant. An observation seen with the 3x3 comes into play here:
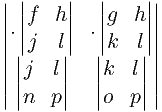 = l
= l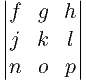
The l term will exist in all cofactors and thus it will drop out as we have seen before.
So that taking any 2x2 subsquare is equivalent to a corresponding underlying determinant of a 3x3 matrix. Thus the above determinant is equal to:

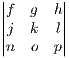 -
-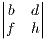
 +
+ 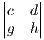

.
In this case the common factor is h which as f in the 3x3 case. We see the a,b,c cofactors all falling out of this equation in the right form. However the d terms are a mess. Gathering all the leftover terms we see:

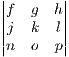 -
-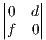
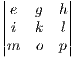 +
+ 

You may be saying to yourself right now wooh way too many terms but look closer. Any term in the 3x3 determinants that come from the 1,1 and 1,2 positions cancels with other terms from elsewhere. Thus the phrase reduces to:

 -
-
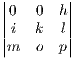 +
+ 

Which put in more familiar notation is:
-dh[e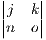 + f
+ f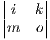 + g
+ g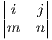 ] ...... the negative sign coming from the fact
the d terms are on the “negative diagonal”
] ...... the negative sign coming from the fact
the d terms are on the “negative diagonal”
Which is of course the partially expanded version of
-dh
which of course is the cofactor matrix of d. Gathering up all the terms in one place we see the 4x4 determinant is
a - b
- b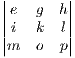 + c
+ c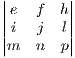 - d
- d
Similarly if you go to a NxN determinant and beyond the problem can be reduced to an N-1 x N-1. Thus recursion is invoked and all higher order determinants are thus known.