The 2 dimensional determinant of a matrix can be interpreted as the area of a parallelogram as shown in the following diagram.

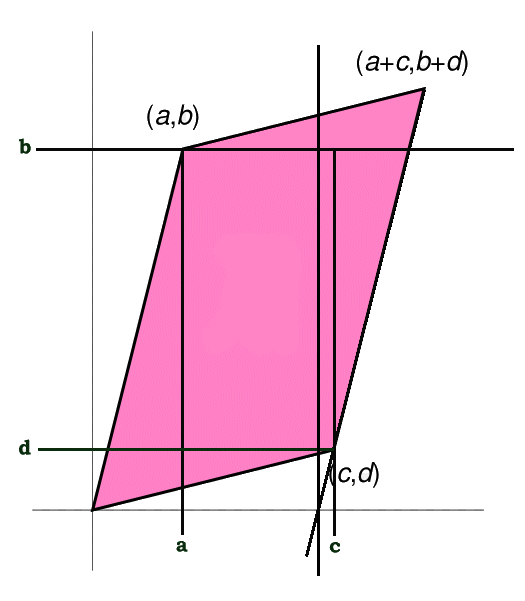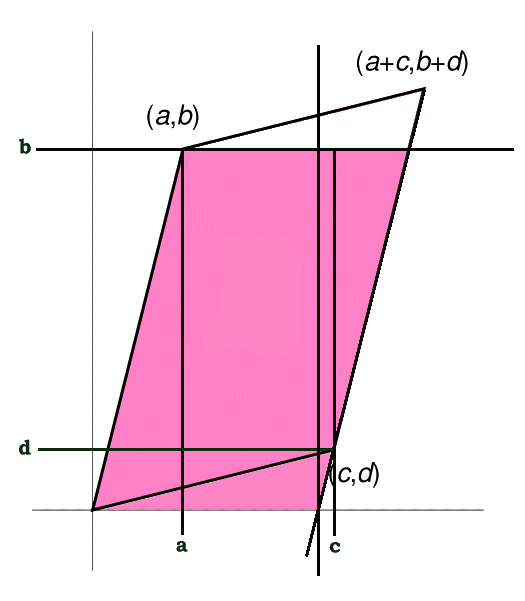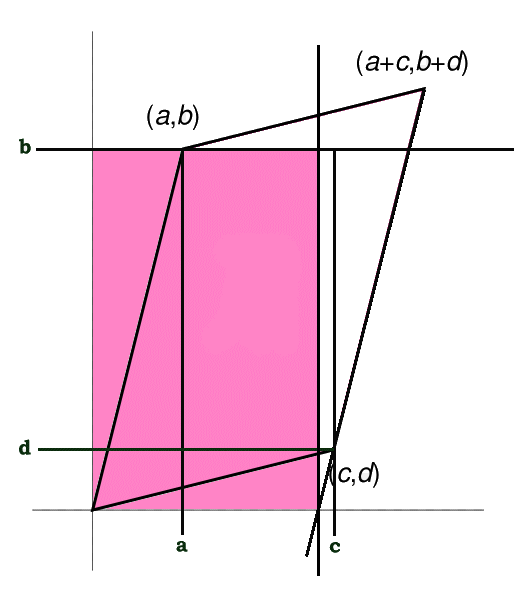
Numeric Example

[pmath]  det (matrix{2}{2}{2 1 1 2}) = 2 * 2 – 1 * 1 = 3 [/pmath]

Compare that with the old fashioned area of two triangles that make up the parallelogram:

[pmath]  Area Paralelogram = 2 * {1/2} * Base * Height [/pmath]

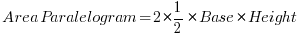
Using Pythagoras:

[pmath] Height = {3/sqrt{2}}  [/pmath]

[pmath] Base  = sqrt{2}  [/pmath]

[pmath] Area Parallelogram = sqrt{2} * {3/sqrt{2}} = 3 [/pmath]

 

 

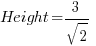
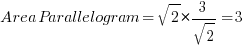
This carries on through higher dimensions.  Below depicts a 3 variable system.

The rows r1, r2, r3 are vectors each. The various summations taken 1, 2 and 3 at a time define a parallelepiped. 

 

The following excerpt is from X and may yield some insight when maximum entropy principle is applied. ( still working on this )