Interpretation of Matrix determinant as hyper volume

A = (matrix{3}{3}{2 0 0 0 3 0 0 0 4 })

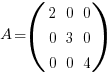
It is easy to see in the case of a brick that the volume = det(A) = 2 * 3 * 4

Assuming that the b vector is equal in the 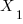X_1 dimension and conveniently using the same values as the system matrix:

$(matrix{3}{3}{2 0 0 0 3 0 0 0 4 })(matrix{3}{1}{X_1 X_2 X_3 }) = (matrix{3}{1}{2 3 4 })$

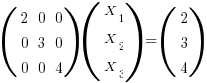
Using the results of the Cramers rule page:

$X_1 = {(matrix{1}{3}{b_1 b_2 b_3}) (matrix{1}{3}{{A_11}^c {A_21}^c {A_31}^c})}/{det(A)}$

$X_1 = { (2 , 3 , 4)(12 , 0 , 0)}/{24} =1$

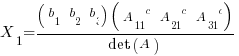
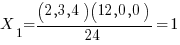
Taking a closer look at this dot product you can see that the only part of the b vector that is important is the 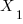X_1 dimension. The zeros in the cofactor vector make the other components irrelevant. This solution can be interpreted as 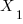X_1 dimension being the number of "brick" volume units that b sweeps out with the cofactor represented hyper-area. The 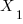X_1 dimension solution of 1 says that 1 brick volume unit is swept out. That is easy to confirm in this case as volume with 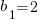b_1 =2 dimension against the area of 3 X 4 is 24.

Matrices with nonzero off diagonal elements

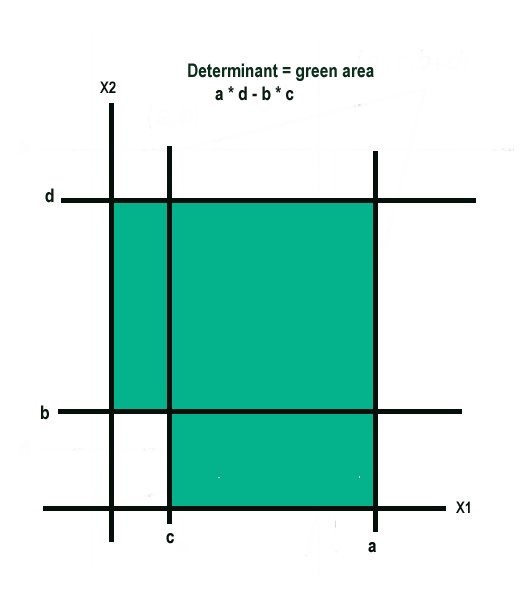
The 2 dimensional determinant of a matrix can be interpreted as the area of a parallelogram as shown in the following diagram.

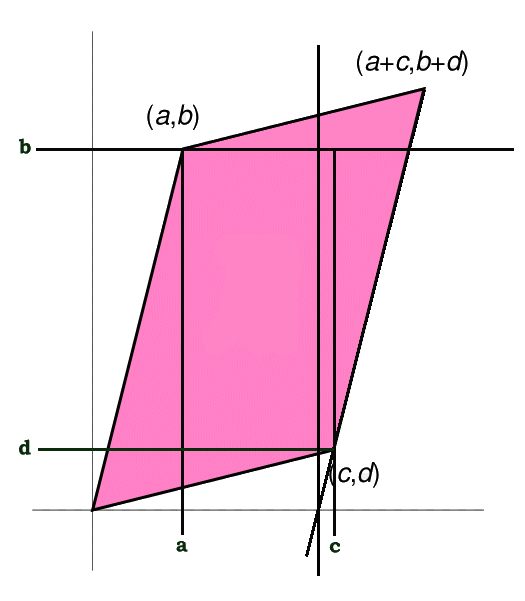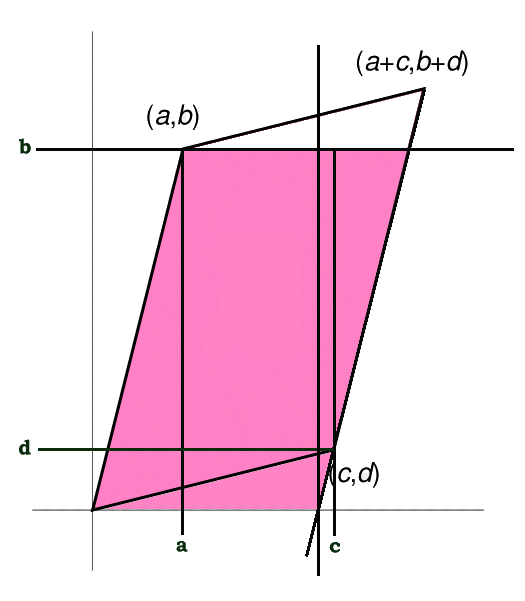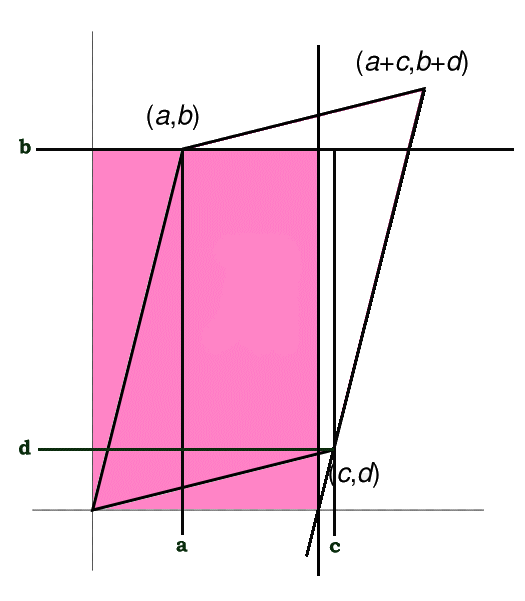
The parallelogram above corresponds to the following matrix

(matrix{2}{2}{a c b d })

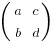
With determinant

a*d - b*c …. the following describes and summarizes the result

Wow! We must be deep in the direction cosines without even noticing! Let us try another point of view.

The area of the parallellogram = Base x Height. We could project the B vector onto a unit vector orthogonal to the base. Or better yet we could project the B vector onto a vector of the same magnitude as the A vector that is orthogonal to A. Well that is easy. Just form that vector by spinning the A vector 90 degrees. The result is < Ay , -Ax >. Now you can calculate the project of B on this orthogonal vector by forming the dot product. That is: < Bx, By > * < Ay, -Ax> = BxAy – ByAx which of course looks like the determinant of a matrix because it is! It corresponds to the following matrix:

$(matrix{2}{2}{B_x A_x B_y A_y })$

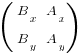
This carries on through higher dimensions. Below depicts a 3 variable system.

The rows r1, r2, r3 are vectors each. The various summations taken 1, 2 and 3 at a time define a parallelepiped.

The following excerpt is from X and may yield some insight when maximum entropy principle is applied. ( still working on this )

Interpretation of Matrix determinant as hyper volume

0 Comments

Leave a Reply