Integral of 1/(1+X^2) Using Geometric Approach – ATan ArcTan

I had to do a trigonometric integral the other day and realized I should be able to see the integral at a glance instead of the mechanistic method I used by substituting 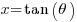x=tan(theta)

W={Delta}{theta}*z

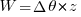
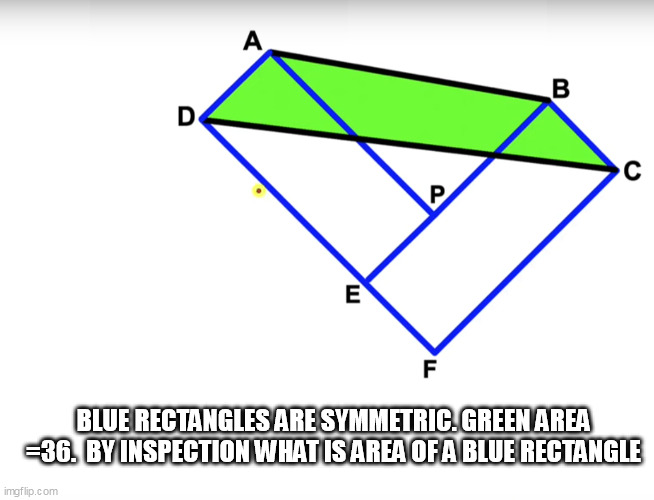
Due to similarity of triangles

{z/1}={{Delta}x}/w

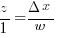
Substituting

{z/1}={{Delta}x}/{{Delta}{theta}*z}

${{Delta}x}/z^2={Delta}{theta}$

${{Delta}x}/{1+x^2}={Delta}{theta}$

$int{.}{.}{.}{{Delta}x}/{1+x^2}=int{.}{.}{.}{Delta}{theta}$

$int{.}{.}{.}{{Delta}x}/{1+x^2}={theta}=atan(x)$

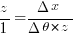
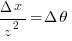
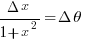
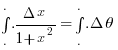
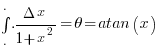
Related Topic

Area of the Rectangle Puzzle

Calculus Proof of the Pythagorean Theorem

Categories: Math

Integral of 1/(1+X^2) Using Geometric Approach – ATan ArcTan

Published by Fudgy McFarlen on June 26, 2014June 26, 2014

0 Comments

Leave a Reply