Basic Polarized Photon Entanglement Experiment

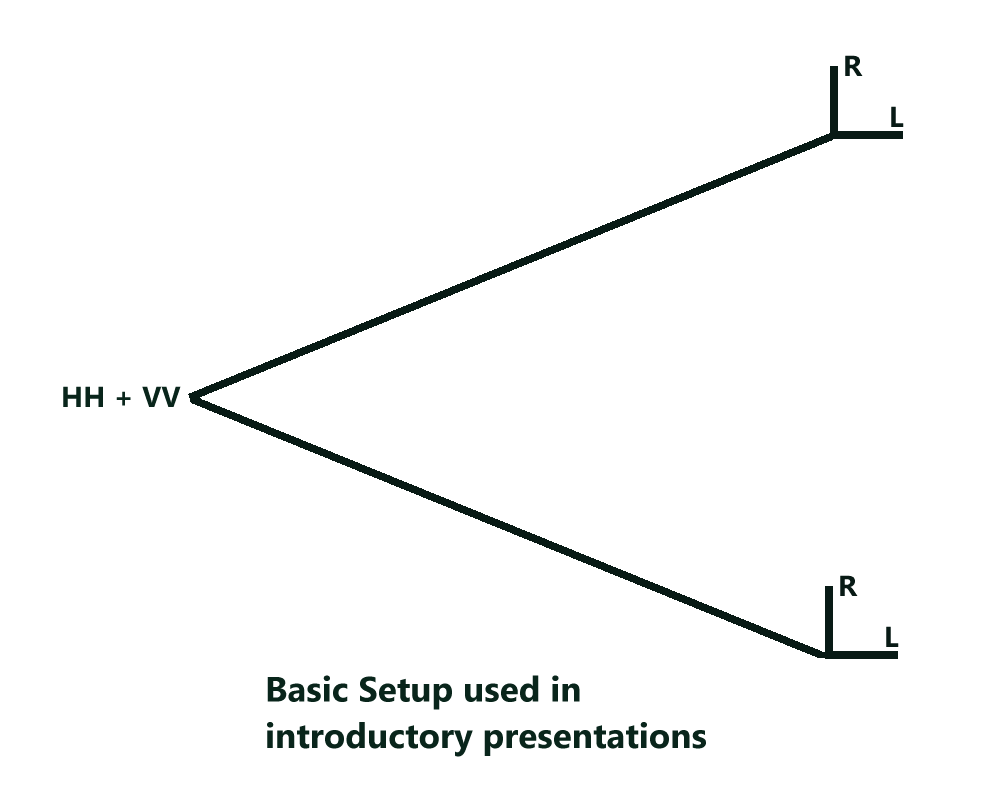
This is the setup used in the Quantum Entanglement and Spooky Action at a distance video presentation with John Bell.

The basic experiment is a pair of entangled photons being put through two different detectors.  The simple version uses the Type -2 detectors of the Mermin Rhetorical homework problem.    The axis are shown in the diagram below. Let H and V be polarization eigenstates for horizontally and vertically polarized photons, and let R and L be polarization eigenstates for two orthogonal  right and left directions at 45 degrees so that

 

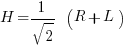
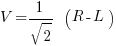
The source produces two photons in the polarization state: 

           this is considered an entangled state because it does not contain a full contingent of states – there are not VH and HV terms.

Thus if both the detectors are type-1 the detectors will show the same results. Either both H or both V.

Substituting the axis transforms:

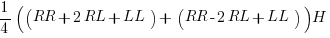
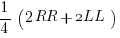
And thus the detectors either see both R or both L 

 

Note how you can not get the critical cancellation without

1. Both UU  AND VV are required to get cancellation.  Without both you do not get the critical term to cancel.  Do we take that to mean they're both ghosted into the detector?  This is more overt in the descriptions with the answer being yes.  They call it a superposition in state.
2. Both photons are depicted as being in each detector.  You need both U & U and V & V for the term to cancel.  Do we take this to mean both photons are ghosted into each detector?  Again it seems to function equivalently to a superposition. This time in space.
3. I take from the above observations that just like in the two slit experiment with single electrons dribbled in – the effect observed will be not be seen should we force a measurement of any of these quantities.